9. 模型安全：后门防御

高效地防御多种后门攻击是一个极具挑战性的任务。一方面，不同后门攻击方法的工作机理可能并不相同，想要深入了解它们的共性具有一定的难度；另一方面设计后门防御策略需要同时考虑多种攻击，通用性比较难实现。目前针对后门攻击的防御策略主要有三种：（1）后门模型检测、（2）后门样本检测 和（3）后门移除。目前，这三类防御方法紧密相关又相对独立，各自完成一个后门防御的子任务。本节将对这三类方法展开介绍。

9.1. 后门模型检测

后门模型检测的目标是判断给定模型是否包含后门触发器，可以根据模型在某种情况下展现出来的后门表现来判断。本节将详细介绍主流后门模型检测方法。

神经净化。 Wang等人 (Wang et al., 2019) 首先提出了基于触发器逆向（trigger reverse engineering）的后门模型检测方法—神经净化（neural cleanse，NC），开启了后门模型检测这一研究方向。该方法假设防御者知晓模型的所有信息，包括模型参数、模型结构等等；此外，防御者还拥有一些可以在该模型下进行正常预测的输入样本。

该方法的核心出发点是：相较于正常类别，翻转后门类别所需要的扰动更少。因此，作者对所有输出类别进行最小像素规模的标签扰动，结合离群点检测方法识别潜在的后门类别，然后利用逆向工程技术重建后门触发器。

具体的，在后门模型检测阶段，NC方法将后门触发器的注入定义为：

(9.1.1)\[\begin{split}A( x, m,\Delta) = x^{'} \\ x_{i,j,c}^{'} = (1- m_{i,j}) \cdot x_{i,j,c} + m_{i,j} \cdot \Delta_{i,j,c},\end{split}\]

其中，\(A(\cdot,\cdot,\cdot)\)表示将后门触发器\(\Delta\)通过掩码\(m\)注入到原始图片\(x\)中的算法（\(\Delta, x \in \mathbb{R}^{h \times w \times c}\)，\(h, w, c\)分别表示图片的高度、宽度和通道数)。掩码\(m \in \mathbb{R}^{h \times w}\)，表示对单一像素位置处的不同通道使用相同的掩码。注意，\(m_{i,j} \in [0, 1]\)，若\(m_{i,j}=1\)，则表示将\(x\)中对应位置的像素替换为\(\Delta\)中对应的像素，若\(m_{i,j}=0\)，则保持\(x\)中像素不变。这里，\(m\)的连续性定义将有利于后续对\(\Delta\)的优化。 对后门触发器\(\Delta\)的重建可以使用有目标对抗攻击方法，即生成\(\Delta\)以使得\(x\)被模型\(f\)预测为目标类别\(y_t\)。此外，假设实际中的后门触发器尺寸较小（这是一个不那么合理的假设），还应该对重建后门触发器的大小进行限制。综合两种优化目标，我们可以得到

(9.1.2)\[\mathop{\mathrm{arg\,min}}_{ m, \Delta} \; \mathbb{E}_{ x\in X} \left[ \mathcal{L}_{\text{CE}}(y_t, f(A( x, m,\Delta))) + \lambda \cdot \| m\|_1\right]，\]

其中，\(\mathcal{L}_{\text{CE}}(\cdot)\)表示交叉熵分类损失函；\(\| m\|_1\)表示掩码的\(L_1\)范数以鼓励\(m\)的稀疏性，生成更小的后门触发器；\(\lambda\)为超参数；\(X\)表示所有正确分类的样本集。可见，该目标函数在所有正确分类的样本上，通过最小化包含后门触发器的样本与目标类别的分类损失，同时限制后门触发器的大小来重建尺寸较小且满足错误分类的后门触发器。该方法对每个类别轮流作为\(y_t\)，并利用Adam优化器 (Kingma and Ba, 2015) 来重建后门触发器。

基于投毒类别更易于进行有目标攻击的假设，可以根据重建的触发器的样式和大小筛选出后门类别。定义逆向得到的每个类别对应的潜在触发器的\(L_1\)范数为\(L=\{L^1, L^2, ..., L^C\}\)，其中\(C\)表示所有类别的数量。那么，可利用中位绝对偏差（median absolute deviation，MAD）指标 (Hampel, 1974) 来衡量离群点，即：

(9.1.3)\[\begin{split}\tilde{L} = \text{median}(L) \\MAD = \text{median}(\|L^i - \tilde{L\|}_1),\end{split}\]

其中，\(\text{median}(\cdot)\)表示取中位数。在得到MAD后，一个类别的异常分数可定义为：

(9.1.4)\[I_i = \frac{\|L^i - \tilde{L\|}_1}{MAD}.\]

那么对于所有类别，我们可以得到\(I = \{I_1, I_2, ..., I_n\}\)来表示每个类别的异常指标。在假设\(I\)为标准正态分布\(\mathcal{N}(0, 1)\)的前提下，我们需要使用

(9.1.5)\[I_i = \frac{1}{\Phi^{-1}(\frac{3}{4})} \cdot I_i \approx 1.4826 \cdot I_i\]

将其异常指标放大到与正态分布样本相同的尺度上，作为标准正态分布的一致估计量（consistent estimator），其中\(\Phi\)表示标准正态分布的累积分布函数(CDF)。因此，当\(I_i > 1.96\sigma\)时有大于95%的概率此类别为离群点，由于为标准正态分布，所以\(I_i > 1.96\)。实际上，NC方法直接使用\(I_i > 2\)作为阈值条件来检测后门类别。

在以上检测过程中，由于需要对每一个类别进行后门触发器的重建，在类别数量很大时会需要较大的计算量。为了进一步降低计算负担，可降低公式 (9.1.2) 的优化迭代次数，先得到一个较为粗糙的重建后门触发器，然后对所有类别进行初筛来降低怀疑为投毒类别的数目。

深度检查。 Chen等人 (Chen et al., 2019) 提出了针对Trojan攻击的防御方法—深度检查（DeepInspect），建立了一种针对模型先验知识较少情况下的后门防御机制。相较于神经净化方法，深度检查方法仅需要模型的类别概率输出，无需训练数据集，因此实用性更高。为了解决没有输入数据的问题，该方法使用模型逆向（model inversion） (Fredrikson et al., 2015) 技术，根据模型的所有输出类别重建了替代数据集。然后，基于替代数据集训练条件生成器（conditional generator），以便快速生成不同类别的后门触发器。最后，该方法根据重建的后门触发器对所有的类别进行异常检测，如果发现后门类别，则使用对抗训练的方式对模型进行修复。下面将详细介绍深度检查方法的检测步骤：

（1）替代数据集生成：深度检查利用模型的反传梯度信息对全零初始化的输入进行优化，使得当前输入的预测类别向指定目标靠近，目标函数为：

(9.1.6)\[c( x) = 1-f( x,y_t)+\text{AuxInfo}( x),\]

其中，\(x\)为全零初始化的模型输入，\(f(\cdot)\)为输入\(x\)预测为类别\(y_t\)的概率，\(\text{AuxInfo}( x)\)表示针对输入\(x\)可利用的其他辅助信息。通过最小化\(c( x)\)以及计算\(c( x)\)关于输入\(x\)的梯度信息，并对\(x\)进行迭代更新以降低\(c( x)\)。模型逆向方法可使得\(x\)被模型\(f\)预测为\(y_t\)类别的概率变大。由此，可针对不同类别生成替代数据集，并将用于下一阶段条件生成器的训练。

（2）后门触发器重建：深度检查使用模型\(f\)作为判别器\(\mathcal{D}\)，使用\(\mathcal{G}\)表示条件生成器，以噪声\(z\)和类别\(y_t\)为输出，生成后门触发器\(\Delta\)，即\(\Delta=\mathcal{G}( z, y_t)\)。为了能够让\(\mathcal{G}\)学习到后门触发器的分布，生成器\(\mathcal{G}\)生成的后门触发器应使得判别器\(\mathcal{D}\)发生错误的分类，即：

(9.1.7)\[\mathcal{D}( x + \mathcal{G}( z, y_t)) = y_t.\]

这里的\(x\)来自于上一阶段生成的替代数据集。 因此，我们使用负对数似然损失（negative loss likelihood, NLL）来衡量生成后门触发器的质量：

(9.1.8)\[\mathcal{L}_{\Delta} = \mathbb{E}_{ x}[\mathcal{L}_{\text{NLL}}(\mathcal{D}(x+\mathbb{g}\mathcal{G}( z,y_t)), t)]\]

此外，还应使得后门样本\(x+\mathcal{G}( z,y_t)\)与原始输入\(x\)无法区分，即增加对抗损失：

(9.1.9)\[\mathcal{L}_{\text{GAN}} = \mathbb{E}_{ x}[\mathcal{L}_\text{MSE}(\mathcal{D}_{prob}( x+\mathcal{G}( z,y_t)), 1)],\]

其中，\(\mathcal{L}_\text{MSE}\)表示均方误差（mean square error，MSE），\(1\)代表原始输入\(x\)在理想情况下的概率输出。

除以上损失外，还应该对后门触发器的大小进行限制，因为这里同样假设大部分触发器的尺寸很小。深度检查使用\(\|\|_1\)对生成的后门触发器大小进行限制，即：

(9.1.10)\[\mathcal{L}_{\text{pert}} = \mathbb{E}_{ x}\left[\max(0, ||\mathcal{G}( z,y_t)||_1 - \gamma)\right],\]

其中，\(\gamma\)控制重建后门触发器\(L_1\)范数约束强度，当\(\|\mathcal{G\|( z,y_t)}_1\)大于\(\gamma\)时，\(\mathcal{L}_{\text{pert}}=||\mathcal{G}( z,y_t)||_1 - \gamma\)，否则\(\mathcal{L}_{\text{pert}}=0\)。

综合以上三个损失，我们得到最终用于训练生成器\(\mathcal{G}\)的损失函数：

(9.1.11)\[\mathcal{L} = \mathcal{L}_{\Delta} + \lambda_1 \mathcal{L}_{\text{GAN}} + \lambda_2 \mathcal{L}_{\text{pert}},\]

其中，超参数\(\lambda_1\)和\(\lambda_2\)用来调节不同损失项的权重。通过调整超参数，可以保证由生成器\(\mathcal{G}\)生成的后门触发器具有95%以上的攻击成功率。

(3)异常检测：与神经净化NC方法类似，深度检查方法基于投毒类别的重建后门触发器小于其他类别这一特点，使用双中值绝对偏差（double median absolute deviation，DMAD）来作为检测标准。MAD方法适用于围绕中位数的对抗分布，而对于左偏、右偏等其他类型的非对称分布而言，效果会发生降低，而利用DMAD则可解决这个问题。定义各类别重建后门触发器的噪声规模大小为\(S=\{S_1, S_2, ..., S_t, ..., S_C\}\)，其中\(C\)为类别总数，那么可以得到整体的中位数为\(\tilde{S} = \text{median}(S)\)。根据\(S\)中每个值与\(\tilde{S}\)的大小关系，可将\(S\)划分为左右两部分：

(9.1.12)\[\begin{split}\begin{split}S^{l} = \{S_i | S_i \in S \And S_i\leq \tilde{S}\} \\S^{r} = \{S_i | S_i \in S \And S_i\geq \tilde{S}\}.\end{split}\end{split}\]

由于假设所测试的后门触发器普遍较小，因此深度检查方法只使用\(S^{l}\)来进行检测，根据式 (9.1.3) 、 (9.1.4) 、 (9.1.5) 对\(S^{l}\)进行计算，并与\(1.96\sigma\)进行比较来得到离群点，确定为后门类别。

通过以上三个步骤，深度检查方法实现了比神经净化更有效的后门触发器重建，且不需要借助额外数据。相较于神经净化方法，深度检查方法在更加苛刻的环境下实现了后门攻击的有效检测，更易于在实际应用场景中的使用。此外，通过重建后门触发器，深度检查方法同样可以在替代数据集以及叠加了重建后门触发器后的“修补”数据集上，对模型进行微调，使得模型具有抵御后门攻击的能力。值得注意的是，尽管深度检查方法声称是一种黑盒防御方法。但事实上，在模型逆向以及生成器的训练过程中，都需要通过模型反传梯度来进行优化，这在严格的黑盒条件下是不允许的。因此，这里并没有把深度检查方法归类为黑盒防御方法。

基于非凸优化和正则的后门检查。 Guo等人 (Guo et al., 2019) 发现当使用不同尺寸、形状和位置的后门触发器来进行后门攻击时，神经净化方法可能会失效。作者认为其主要原因在于后门子空间中存在多个后门样本，而基于触发器逆向的神经净化方法可能会搜索到与后门触发器无关的后门样本。为此，作者提出了基于非凸优化和正则的后门检查（Trojan backdoor inspection based on non-convex optimization and regularization，TABOR）方法，通过多个训练正则项来改善原始神经净化的优化目标。下面将对增加的正则化项进行详细介绍。

在利用优化器（式 (9.1.1) ）重建后门触发器的过程中，会出现稀疏触发器（scattered trigger）和过大触发器（overly large trigger）的问题。稀疏触发器在整个图像区域中比较分散，无法聚拢到某一个特定的位置；而过大触发器在图像区域中所占的面积过大，远大于正常后门触发器的尺寸。因此，需要对重建后门触发器的面积大小以及聚拢程度进行限制。

针对过大触发器，TABOR定义如下正则化项来惩罚面积过大：

(9.1.13)\[R_1( m, \Delta) = \lambda_1 \cdot R_{\text{elastic}}(vec( m)) + \lambda_2 \cdot R_{\text{elastic}}(vec((1- m) \odot \Delta)),\]

其中，\(vec(\cdot)\)表示将矩阵转换为向量；\(R_{\text{elastic}}(\cdot)\)表示向量的\(L_1\)和\(L_2\)范数之和；\(\lambda_1\)和\(\lambda_2\)为超参数。这里的\(m\)表示后门触发器的掩码，\(\Delta\)表示重建的后门触发器。公式 (9.1.13) 在对掩码\(m\)中非零项进行惩罚的同时，也对掩码0值区域的重建后门触发器的非零项进行惩罚，从而解决过大的问题，缩小后门子空间中后门样本的数量。

针对稀疏触发器，TABOR定义如下正则化项来惩罚稀疏性：

(9.1.14)\[\begin{split}R_2(v, \Delta) = \lambda_3 \cdot s( m) + \lambda_4 \cdot s((1- m) \odot \Delta) \\s( m) = \sum_{i,j}( m_{i,j}- m_{i,j+1})^2 + \sum_{i,j}( m_{i,j}- m_{i+1,j})^2,\end{split}\]

其中，\(\lambda_3\)和\(\lambda_4\)为超参数，\(s(\cdot)\)为平滑度量函数，用来表示零或者非零值的密度，\(m_{i,j}\)表示第\(i\)行第\(j\)列的元素。可以看到，当重建的后门触发器越稀疏时，其\(R_2\)值会更高。因此，TABOR中使用该正则项进一步缩小搜索空间。

此外，重建的后门触发器有时还会遮挡图像中的主要物体，称之为遮挡触发器（blocking trigger），但后门触发器的成功往往不依赖于遮盖主要物体，而在于高响应值。因此，TABOR定义如下正则化项来避免遮盖主要物体：

(9.1.15)\[R_3 = \lambda_5 \cdot \mathcal{L}(f( x \odot (1- m)), y),\]

其中，\(y\)表示\(x\)预测的正确类别；\(x\odot(1- m)\)表示触发器位置以外的像素；\(\lambda_5\)为超参数。如果\(x\)在去除了触发器区域像素后仍能正确分类，则表示后门触发器的位置远离模型决策所依赖的关键区域，从而实现不遮盖主要物体的目的。

最后，还存在叠加触发器（overlaying trigger）的情况，重建触发器与真实触发器具有一定程度的叠加。为了缓解该现象，TABOR从特征重要性的角度入手，要求重建的后门触发器可以满足攻击模型的目的，从而去除不重要的部分，使得重建后的后门触发器更加精简、准确。该正则项定义为：

(9.1.16)\[R_4 = \lambda_6 \cdot \mathcal{L}(f( m \odot \Delta), y_t),\]

其中，\(y_t\)为攻击目标类别；\(\lambda_6\)为超参数。基于此，TABOR可在较为重要的区域里重建后门触发器。

将以上四个正则化项加入到NC方法的目标函数（公式 (9.1.1) ）后即可生成更加准确的后门触发器。当然，最后还需要通过异常检测来找到后门类别和后门触发器。相较于神经净化的\(L_1\)距离筛选法，TABOR给出了更加精确、具体的度量定义：

(9.1.17)\[\begin{split}\begin{aligned}A( m_t, \Delta_t) = \log(\frac{\|vec(f^{(t)})\|_1}{d^2}) + \log (\frac{s(f^{(t)})}{d\cdot(d-1)}) \\- \log(acc_{\text{att}}) - \log(acc_{\text{crop}}) - \log(acc_{\text{exp}})，\end{aligned}\end{split}\]

其中，\(m_t\)和\(\Delta_t\)可构成类别\(y_t\)的后门触发器，即\(m_t \odot \Delta_t\)；\(acc_{\text{att}}\)表示将重建后门触发器注入到干净样本中后导致的错误分类率；\(acc_{\text{crop}}\)为在从污染图像中裁剪出相应的后门触发器后得到的预测准确率；\(acc_{\text{exp}}\)表示仅将污染图像中的基于可解释性得到的重要特征输入模型后得到的预测准确率。对于前两项，定义\(f_{i,j}^{(t)}=\mathbb{1}( m_t \odot \Delta_t)_{i,j}>0\)，通过\(\|vec(f^{(t)}\|_1\)以及\(s(f^{(t)})\)来实现稀疏度量和平滑性度量；\(d\)表示图像的维度，用来归一化。 在得到每个类别重建触发器的度量指标后，可利用MAD（公式 (9.1.3) 、 (9.1.4) 和 (9.1.5) ）进行异常检测。

针对过多的超参数（\(\{\lambda_1, \lambda_2, \lambda_3, \lambda_4, \lambda_5, \lambda_6\}\)），TABOR设计了一种超参增强机制，缓解超参对触发器重建性能的影响。在优化的初始阶段，将超参数初始化为较小的值，也就是说在此阶段中正则化项对于目标函数的贡献接近0；之后会将当前重建的后门触发器注入到干净样本中以获得污染样本，并将污染样本输入到模型中获取错误分类率，只有当错误分类率达到一个确定的阈值时，才会将超参数乘上固定的扩大因子\(\gamma\)；否则，将会除以\(\gamma\)。以上操作会重复进行，直到正则化项的值趋于稳定，即\(|R_t^{k-1} - R_t^{k}| < \epsilon\)，其中\(R_t^k\)表示在第\(k\)次迭代中第\(t\)个正则项的值；\(\epsilon\)为一个较小的常数。

TABOR在神经净化框架下，增加了多种正则化项来解决其在后门触发器重建过程中存在的问题。此外，还从多个角度设计了更加全面的度量标准，以获得更好的异常检测性能。结果显示，TABOR方法相较于神经净化方法在后门触发器重建及检测上取得了更好的效果。

数据受限下的检测。 Wang等人 (Wang et al., 2020) 在数据受限（Data-limited）及无数据（data-free）的情况下分别提出了有效的后门类别检测方法—DL-TND（TrojanNet detector）和DF-TND。其中，DL-TND在每个类别仅有一张图像的条件下，针对每个类别分别计算其非目标通用对抗噪声（untargeted universal adversarial noise）和单一图像的有目标对抗噪声（targeted adversarial noise），并比较两种噪声之间的差异，从而识别后门类别。DF-TND不使用原始图像，而利用随机图像作为检测数据，它通过最大化中间层神经元激活来获取扰动图像，然后根据随机图像与扰动图像在输出概率上的差异来检测后门类别。下面将分别对DL-TND和DF-TND进行详细介绍。

类似于公式 (9.1.1) ，DL-TND定义添加了后门触发器的图片为：

(9.1.18)\[\hat{ x}( m, \Delta) = (1- m) \cdot x + m \cdot \delta,\]

其中，\(0 \leq \Delta \leq 255\)为触发器噪声，\(m \in\{0,1\}\)为定义了添加位置的二值掩码。 在数据限制下，可针对每个类别获取一张照片，因此DL-TND使用\(D_k\)表示类别\(k\)的图片集合，\(D_{k-}\)表示不同于类别\(k\)的其他图片集合。

首先，DL-TND利用\(D_{k-}\)数据集获取非目标通用对抗噪声，即在\(D_{k-}\)中增加噪声\(u^{(k)}\)使得模型发生错误分类。与此同时，\(u^{k}\)不会影响\(D_k\)在模型上的分类。通过模拟后门触发器只干扰\(D_{k-}\)样本的特性，来进行噪声模拟。形式化定义如下：

(9.1.19)\[\mathop{\mathrm{arg\,min}}_{ m, \Delta} \ \ \mathcal{L}_{\text{atk}}(\hat{ x}( m, \Delta); D_{k-}) + \hat{\mathcal{L}}_{\text{atk}}(\hat{ x}( m, \Delta); D_{k}) + \lambda \| m\|_1,\]

其中，\(\lambda\)为超参数，\(\| m\|_1\)用来保证稀疏性。公式中的前两项损失分别定义为：

(9.1.20)\[\begin{split}\begin{aligned}\mathcal{L}_{\text{atk}}(\hat{ x}( m, \Delta); D_{k-}) = \sum_{ x_i \in D_{k-}} \max\{f_{y_i}(\hat{ x}_i( m, \Delta)) - \max_{t \neq y_i}f_t(\hat{ x}_i( m, \Delta)), -\tau\} \\\hat{\mathcal{L}}_{\text{atk}}(\hat{ x}( m, \Delta); D_{k}) = \sum_{ x_i \in D_{k}} \max\{\max_{t \neq y_i}f_t(\hat{ x}_i( m, \Delta)) - f_{y_i}(\hat{ x}_i( m, \Delta)), -\tau\},\end{aligned}\end{split}\]

其中，\(y_i\)为\(x_i\)的真实类别，\(f_t(\cdot)\)表示类别\(t\)的预测值，\(\tau \geq 0\)为超参，用来界定攻击的最低置信程度。

公式 (9.1.20) 参考了CW攻击 (Carlini and Wagner, 2017) 的非目标攻击形式，使得\(D_{K-}\)发生非目标错误分类而不影响\(D_k\)的正确分类。 此时，DL-TND会对每个图像\(x_i \in D_{k-}\)分别计算目标对抗噪声，使得\(\hat{ x}_i( m, \Delta)\)会被模型错分类为\(k\)。DL-TND认为目标攻击与非目标通用攻击一样，偏向使用后门捷径（backdoor shortcut）来生成对抗噪声。目标攻击定义如下：

(9.1.21)\[\mathop{\mathrm{arg\,min}}_{ m, \Delta} \ \ \mathcal{L}^{'}_{\text{atk}}(\hat{ x}( m, \Delta); D_{k-}) + \lambda\| m\|_1,\]

其中，第一项同样采用CW攻击形式，定义为：

(9.1.22)\[\mathcal{L}^{'}_{\text{atk}}(\hat{ x}( m, \Delta); D_{k-}) = \sum_{ x_i \in D_{k-}} \max\{\max_{t \neq k}f_t(\hat{ x}_i( m, \Delta)) - f_{k}(\hat{ x}_i( m, \Delta)), -\tau\}.\]

通过上式可针对每个类别\(k\)和对应的图像\(x_i\)生成噪声\(s^{k,i} = ( m^{k,i}, \Delta^{k,i})\)。 因此，根据相似性假设，当某个类别中存在后门触发器时，\(u^{k}\)和\(s^{k,i}\)应该具有高度的相似性。DL-TND叠加两种噪声后，在模型中间层的特征上计算余弦相似度。对于\(x_i \in D_{k-1}\)分别执行上述步骤，可以得到相似度得分向量\(v_{\text{sim}}^{k}\)。 最后，可通过MAD或者人为设定的阈值进行后门类别检测。

在无数据的情况下，可通过最大化随机输入\(x\)在模型中间层的神经元激活来生成噪声，其优化目标定义为：

(9.1.23)\[\mathop{\mathrm{arg\,max}}_{ m, \Delta, w} \sum_{i=1}^{d}[ w_i r_i(\hat{ x}( m, \Delta))] - \lambda \| m\|_1,\]

其中，\(r_i(\cdot)\)表示第\(i\)维的神经元激活值，\(0 \leq w \leq 1\)且\(\sum_i w = 1\)，用来调整不同神经元的重要性，\(d\)表示模型中间层的维度。上式对于\(n\)个随机输入可以优化得到\(n\)个掩码和触发器对\(\{p^{(i)} = ( m^{(i)}, \Delta^{(i)})\}_{i=1}^{n}\)。

最后，基于\(\{p^{(i)}\}_{i=1}^{n}\)，通过比较随机输入与其后门版本在模型输出上的差异来检测后门类别：

(9.1.24)\[R_k = \frac{1}{N} \sum_{i}^{N}[f_k(\hat{ x_i}(p^{(i)})) - f_k( x_i)].\]

根据上式可计算每个类别输出差值，进而可基于预先设定的阈值来进行检测，\(R_k\)值越大表示后门风险越大。

9.2. 后门样本检测

后门样本检测的目标是识别训练数据集或者测试数据集中的后门样本，其中对训练样本的检测可以帮助防御者清洗训练数据，而对测试样本的检测可以在模型部署阶段发现并拒绝后门攻击行为。下面介绍几种经典的后门样本检测方法。

频谱指纹。 为了检测训练数据中可能存在的后门样本，Tran等人 (Tran et al., 2018) 在2018年提出了频谱指纹（spectral signature, SS）方法。该方法观察到后门样本和干净样本在深度特征的协方差矩阵上存在差异，故可以通过检测这种差异来过滤后门样本。

算法 图9.2.1 中给出了SS方法的检测流程。具体来说，给定训练样本\(D\)，首先训练得到神经网络\(f\)。然后，按照类别遍历，并提取每个样本的特征向量并计算每类样本的特征均值。接下来，对深度特征的协方差矩阵进行奇异值分解，并使用该分解计算每个样本的异常值分数。根据异常检测规则移除数据集中异常值高于\(1.5 \epsilon\)的样本（后门样本），最终返回一个干净的训练数据集\(D_{\text{clean}}\)。

图9.2.1 频谱指纹（SS）检测算法

图9.2.2 激活聚类（AC）检测算法

激活聚类。 Chen等人 (Chen et al., 2018) 提出了一种基于激活聚类（activation clustering，AC）的方法来过滤训练数据中的潜在后门样本。该方法的主要思想是：后门特征和干净特征之间存在差异，且这种差异在深度特征空间中会更加显著。因此，可以基于聚类方法来自动分离后门特征，进而帮助检测后门样本。

算法 图9.2.1 中给出了AC方法的检测流程。该方法首先在后门训练数据集\(D\)上训练模型\(f\)，然后对所有训练样本\(x_{i} \in D\)提取其特征激活（默认选取模型最后一个隐藏层的输出），得到一个包含所有特征激活的集合\(A\)。然后，对得到的特征激活进行降维，并利用聚类方法对训练数据集进行聚类分析。实验表明，通过分析最后一层隐藏层的激活分布就能够有效检测后门数据。

值得注意的是，AC方法假定训练数据中一定存在后门样本，所以在激活聚类时默认将整个数据集划分为两个数据簇。作者提出了三个后门数据簇的判别依据：（1）重新训练分类；（2）聚类簇的相对大小；（3）轮廓的分数。实验表明，比较聚类簇数据规模的相对大小可以作为一个简单有效的评判依据。

认知蒸馏。 后门样本会误导模型去识别任务无关的后门触发器样式，这使得模型的认识逻辑发生错误，模型在后门样本上的注意力区域发生偏移。但事实并非如此，我们发现模型在后门样本上依然会关注一部分有意义的区域。这就需要一种技术可以精准地剖离模型的核心认知逻辑，去除不重要的甚至是噪声的注意力，从而可以暴露模型真正关注的地方。基于此种想法，Huang等人 () 提出 认知蒸馏 （cognitive distillation，CD）的概念，给定一个输入样本（训练样本或测试样本皆可），此方法提取模型得到同样输出所需要的最少输入信息。决定模型输出的最小输入模式又称为 认知模式 （cognitive pattern），它揭示了模型推理结果背后所隐藏的决定性因素。

具体来说，认知蒸馏方法通过解决一个最小化问题来从一个输入样本\(x\)中蒸馏出其认知模式。优化问题具体定义如下：

(9.2.1)\[\mathrm{arg\,min}_{m}||f_{\theta}(x) - f_{\theta}(x_{cp})||_1 + \alpha ||m||_1 + \beta \cdot TV(m)\]

(9.2.2)\[x_{cp}=x\odot{m} + (1-m)\odot\delta,\]

其中，\(m\)是输入掩码，\(f_{\theta}\)是模型的逻辑或者概率输出，\(x_{cp}\)是认知模式，\(\delta \in [0,1]^c\)是一个\(c\)-维的随机向量，\(\odot\)是元素对应乘积操作，\(TV(\cdot)\)是总变差（TV）损失，控制优化所得掩码的平滑程度（我们希望得到局部平滑的关键区域），\(\beta\)为平衡TV损失的超参数。

图9.2.3 在干净或者后门图片上通过认知蒸馏方法提取出来的认知模式

图 图9.2.3 展示了认知蒸馏算法在干净图片以及被11种后门攻击算法攻击过的图片上抽取到的掩码和模式。可以看到，模型在被添加了后门触发器的图片上的认知机理大都由后门触发器决定，触发器对应的位置对模型的输入起到了决定性的作用。此外还发现，有些全图的触发器，比如Blend、CL、FC、DFST等攻击所使用的触发器，只是部分在起作用，而并不需要全图大小的触发器。基于此发现，Huang等人对已有攻击的触发器进行了进一步简化，发现简化后的触发器跟原触发器攻击效果相似，有的甚至还变更强了。

基于式 eq_cd 优化得到的掩码\(m\)，Huang等人构建了一个后门样本检测器，将检测掩码过小的样本检测为后门样本。检测原理是基于图 图9.2.3 中的发现：后门样本的认知模式往往更简单，即模型通过过于简单的模式对样本进行了结果预测。在3个数据集、6个模型以及12种后门攻击上的检测结果表明，认知蒸馏方法可以将训练集中后门样本的平均检测AUC从此前最优的84.62%提升到96.45%，将测试集中后门样本的平均检测AUC从此前最优的82.51%提升到了94.90%。

后门数据只是问题数据的一种，其他的问题数据包括投毒样本、损坏样本、对抗样本等等，都会误导模型产生错误的推理逻辑。如果能够准确且唯一地确定模型的主要推理依据，那么就可以判断模型的决策是否存在问题。如果能进一步对有问题的推理逻辑进行共性建模，那么就可以构建服务于模型推理阶段的问题数据过滤和纠正器。 未来大模型会被广泛使用，它们的训练代价很高，难以通过重训练或者微调的方式来保证全面的鲁棒性，所以迫切地需要检测防御方法来保障其安全稳定的运行。比如OpenAI、谷歌等一些公司在发布生成式大模型（如ChatGPT）时都会启动一系列检测模型，以此来防止模型因受到攻击或者引诱而生成有害的内容。

9.3. 后门移除

后门检测之后需要后门移除方法将检测出来的后门从模型中清除掉，以完成模型净化。如此，后门移除的目标主要有两个：（1）从后门模型中移除后门；（2）保持模型的正常性能不下降。后门移除对后门防御至关重要，在实际应用场景中可以起到重要的作用，所以后门防御的大部分工作都是围绕后门移除进行的。现有的后门移除方法大致可以分为两类：（a）训练中移除，在模型的训练过程中检测出潜在的后门样本，并阻止模型对这些样本的学习；（b）训练后移除，从后门模型中移除掉已经被植入的后门触发器，以还原模型的纯净功能。

9.3.1. 训练中移除

反后门学习。 如何从被污染的数据中学习一个干净的模型是一个挑战的问题。Li等人 (Li et al., 2021) 首次提出了反后门学习（anti-backdoor learning，ABL）的概念，通过设计鲁棒的训练方法让模型可以在被后门毒化的数据集上正常训练，自动避开对后门样本的学习，最终得到一个干净无后门的模型。

具体而言，ABL方法首先揭示了两个后门攻击固有的弱点：（1）后门样本比干净样本被模型学的更快，而且后门攻击越强，模型在后门样本上的收敛速度就越快；（2）后门触发器与后门标签之间存在强关联。显然，被部分毒化的数据集既包含干净数据子集（\(D_c\)）也包含后门数据子集（\(D_b\)）。那么，我们可以将基于毒化数据集的模型训练看做是两个学习任务平行进行，即定义在\(D_c\)上的干净任务（clean task）和定义在\(D_b\)上的后门任务（backdoor task）。对于图像分类任务来说，在毒化数据集上的模型训练等于优化以下目标：

(9.3.1)\[\begin{aligned}\mathcal{L} =\mathbb{E}_{( x,y)\sim D_c}[\mathcal{L}_{\text{CE}}(f( x,y))]+\mathbb{E}_{( x,y)\sim D_b}[\mathcal{L}_{\text{CE}}(f( x,y))],\end{aligned}\]

其中，\(\mathcal{L}_{\text{CE}}(\cdot)\)表示交叉熵损失函数。然而，由于在训练过程中我们无法得到毒化部分数据\(D_b\)，所以无法直接求解公式 (9.3.1) ，也就无法阻挡模型对后门数据的学习。为此，ABL将整个训练过程划分为后门隔离（backdoor isolation）和后门反学习（backdoor unlearning）两个阶段，如式 (9.3.2) 所示：

(9.3.2)\[\begin{split}\mathcal{L}_{\text{ABL}}^t=\begin{cases}\mathcal{L}_{\text{LGA}}=\mathbb{E}_{( x,y)\sim D}[ sign(\mathcal{L}_{\text{CE}}(f( x),y)-\gamma) \cdot \mathcal{L}_{\text{CE}}(f( x),y)] 0 \leq t \leq T_{te} \\\mathcal{L}_{\text{GGA}}=\mathbb{E}_{( x,y)\sim \widehat{D_c}}[\mathcal{L}_{\text{CE}}(f( x),y)]-\mathbb{E}_{( x,y)\sim \widehat{D_b}}[\mathcal{L}_{\text{CE}}(f( x),y)] T_{te} \leq t \leq T\end{cases}\end{split}\]

其中，\(t\in [0,T-1]\)为当前的迭代次数，\(sign(\cdot)\)表示符号函数，\(\mathcal{L}_{\text{LGA}}\)表示第一阶段损失函数，\(\mathcal{L}_{\text{GGA}}\)为第二阶段损失函数。上式包含两个关键的技术：局部梯度上升（local gradient ascent，LGA）和全局梯度上升（global gradient ascent，GGA)。

局部梯度上升可以巧妙的应对后门攻击的第一个弱点，即后门数据学的更快（训练损失下降的极快）。LGA通过将训练样本的损失控制在一个阈值\(\gamma\)附近，从而让后门样本穿过这个阈值而普通样本无法穿过。具体的，当样本的损失低于\(\gamma\)时，LGA会增加其损失到\(\gamma\)；否则，其损失值保持不变。同时，在该阶段会根据样本的损失值将训练集划分为两部分，损失值较低的被分到（潜在）后门数据集\(\widehat{D_b}\)，其余的被分到干净数据集\(\widehat{D_c}\)，划分（检测）比率\(p=|\widehat{D_b}| / |D|\)可以被设定于低于数据真正的中毒率（比如训练数据的1%）。

全局梯度上升针对后门攻击的第二个弱点，即后门攻击触发器与后门类别存在强关联。实际上，当后门触发器被检测出来的时候，它已经被植入到模型当中了，所以需要额外的步骤将其从模型中移除。全局梯度上升可以做到这一点，它的目标是借助第一阶段隔离得到的少量潜在后门样本\(\widehat{D_b}\)，对后门模型进行反学习（unlearning），通过最大化模型在数据\(\widehat{D_b}\)上的损失，让模型主动遗忘这些样本。

ABL方法为工业界提供了在不可信或者第三方数据上训练良性模型的新思路，可帮助公司、研究机构或政府机构等训练干净、无后门的人工智能模型。此外，ABL鲁棒训练方法有助于构建更加安全可信的训练平台，为深度模型的安全应用提供有力保障。

9.3.2. 训练后移除

一般来说，后门模型的修复可以基于重建的后门触发器进行，因为只有掌握了后门触发器的信息才能知道需要从模型中移除什么功能。但是触发器重建通常比较耗时，所以现有的训练后移除方法大都不基于触发器重建进行，而是假设防御者有少量的干净数据用以模型净化。这些少量的干净数据可以用来对模型进行微调、蒸馏等操作，以达到修复模型的目的。

精细剪枝方法。 Liu等人 (Liu et al., 2018) 提出了精细剪枝（fine-pruning）方法，整合了剪枝和微调两个技术，可有效消除模型中的后门。剪枝是一种模型压缩技术，可以用来从后门模型中裁剪掉与触发器关联的后门神经元，从而达到模型净化的效果。因为后门神经元只能被后门数据激活，所以在干净数据上休眠的神经元就极有可能是后门神经元，需要进行剪枝。剪枝后的模型会发生一定程度的性能下降，所以需要在少量干净数据（也称为防御数据）上进行微调，恢复其在干净样本上的性能。精细剪枝方法虽然很简单，确实很简单直观，所以经常被用来作为基线方法比较。当然，精细剪枝方法的防御性能并没有很好，尤其是在面对一些复杂的攻击时，往往只能将攻击成功率从接近100%降低到80%左右。

基于GAN的触发器重建。 Qiao等人 (Qiao et al., 2019) 对触发器重建进行了研究，发现重建后的后门触发器往往来自于连续的像素空间，且重建的后门触发器比初始触发器的攻击强度甚至还要高，这表明重建触发器分的布可能包含了原始触发器，但单一触发器无法有效表达整个触发器空间。因此，Qiao等人提出了基于最大熵阶梯逼近（max-entropy staircase approximator，MESA）的生成对抗网络（GAN），以生成有效后门触发器的分布\(p_{ r}\)，该分布甚至对于攻击者而言都是未知的。为了处理该问题，MESA使用替代模型\(f'\)来近似有效后门触发器分布，这里\(f'\)返回给定后门触发器的攻击成功率。且使用\(N\)个子生成模型来分别学习分布\(p_{ r}\)的不同部分\(\mathcal{X}_i=\{ x:f'( r)>\beta_i\}\)，其中\(r\)表示触发器，\(\beta_i\)表示第\(i\)个子生成模型的阈值，且满足\(\beta_{i+1}>\beta_i\)，\(\mathcal{X}_{i+1} \subset \mathcal{X}_i\)（因为\(\mathcal{X}_i\)的定义是\(f'( r)>\beta_i\)）。 每个子生成模型的优化函数为：

(9.3.3)\[\begin{split}\begin{aligned}\mathop{\mathrm{arg\,max}}_{G:\mathbb{R}^{n} \rightarrow \mathcal{X} } h(G(Z)) \\\text{s.t.}\ G_i(Z) \in \mathcal{X}_i,\end{aligned}\end{split}\]

其中，\(Z\)表示随机噪声向量，\(h(\cdot)\)表示输出熵。可由互信息神经估计（mutual information neural estimator，MINE） (Belghazi et al., 2018) 得到的互信息来代替。当生成模型确定时，有：

(9.3.4)\[h(G(Z)) = I(X;Z),\]

其中，\(I(\cdot;\cdot)\)表示互信息。 根据支持向量机 (Cortes and Vapnik, 2004) 中的松弛技术，基于MESA建模有效后门触发器分布的优化目标为：

(9.3.5)\[\mathcal{L}=\max(0, \beta_i - f' \circ G_{\theta_i}( z)-\alpha I_{T_i}(G_{\theta_i}( z); z^{'})),\]

其中，\(z, z^{'}\)为独立的用于互信息估计的随机变量，\(I_{T_i}\)为由统计网络\(T_i\)作为参数的互信息估计器；\(\alpha\)为超参数，用来平衡熵最大化的软约束。 当集成多个子生成模型后，可实现对后门触发器空间的有效建模。为修复该后门漏洞，MESA方法在后门触发器空间中生成多个后门触发器，并以此缓解模型后门。

模式连通修复。 Zhao等人 (Zhao et al., 2020) 利用损失景观中的模式连通性(mode connectivity)对深度神经网络的鲁棒性进行研究，并提出了一种新颖的后门模型的修复方法—模式连通修复（mode connectivity repair，MCR）。直观来讲，模式连通指的是模型从一套参数（比如包含后门的参数，有后门但干净准确率高）到另一套参数（比如干净模型参数，无后门但干净准确率低）往往遵循特定的轨迹，那么在这个轨迹上进行合理的选择就可以得到一套无后门且性能下降不多的参数。

具体的，MCR首先选取两个后门模型作为端点模型，然后利用模式连接将两个端点模型的权重连接起来，并在少量干净样本上优化此路径，最终得到一条包含最小损失权重的路径。作者指出，该路径上的最小损失点（通常是中心点）对应的模型参数不包含后门触发器且干净准确率得到了保持。连接两个后门模型是一种模型参数混合（model mixup）的思想（类比于数据混合增广），不过这里混合路径是优化得到的，可以巧妙的避开两个后门模型的缺点（也就是后门），同时最大化二者的优点（也就是干净准确率）。

作者主要探索了多边形连通路径（polygonal chain）和贝兹曲线连通路径（Bézier curve）两种模式，其中连通函数定义为\(\phi_{\theta}(t)\)。具体的，假定两个端点模型的权重分别表示为\(\omega_{1}\)和\(\omega_{2}\)，连接路径的弯曲程度定义为\(\theta\)，多边形连通函数定义为：

(9.3.6)\[\begin{split}\phi_{\theta}(t)=\left\{\begin{array}{cc}2\left(t \theta+(0.5-t) \omega_{1}\right), 0 \leq t \leq 0.5 \\2\left((t-0.5) \omega_{2}+(1-t) \theta\right), 0.5 \leq t \leq 1.\end{array}\right.\end{split}\]

Bezier曲线为有效控制连接路径的平滑度提供了方便的参数化形式。给定端点参数为\(\omega_{1}\)和\(\omega_{2}\)，二次贝兹曲线定义为：

(9.3.7)\[\phi_{\theta}(t)=(1-t)^{2} \omega_{1}+2 t(1-t) \theta+t^{2} \omega_{2}, \;\; 0 \leq t \leq 1.\]

需要注意的是，对于后门模型修复，上述路径优化仅需要将端点模型替换为后门模型即可。实验表明，通过少量干净样本优化此连通路径，并选择最小损失路径对应的参数作为模型的鲁棒参数，可以有效从模型中移除后门，同时保证较少的准确率损失。

神经注意力蒸馏。 既然有少量干净数据，那么除了剪枝微调以外，模型蒸馏方法也可以用于后门防御，而且蒸馏往往比微调更高效。基于此想法，Li等人 (Li et al., 2021) 提出了神经注意力蒸馏（neural attention distillation, NAD）方法，通过使用知识蒸馏并借助少量干净数据进行后门触发器的移除。因为知识蒸馏涉及两个模型（即教师模型和学生模型），那么基于知识蒸馏的后门防御就需要选择恰当的教师和学生。

NAD方法利用在防御数据上微调过后的模型作为教师模型，因为防御数据是干净的，所以此步微调已经移除了教师模型中的部分（不是全部）后门。然后，NAD利用教师模型引导学生模型（未经过任何微调的原始后门模型）在防御数据上再次进行蒸馏式微调，使学生模型的中间层注意力与教师模型的中间层注意力一致，从而在学生后门模型中移除后门触发器。NAD的整体流程如图 图9.3.1 所示，该方法的核心在于寻找合适的注意力表征来保证蒸馏防御的有效性。

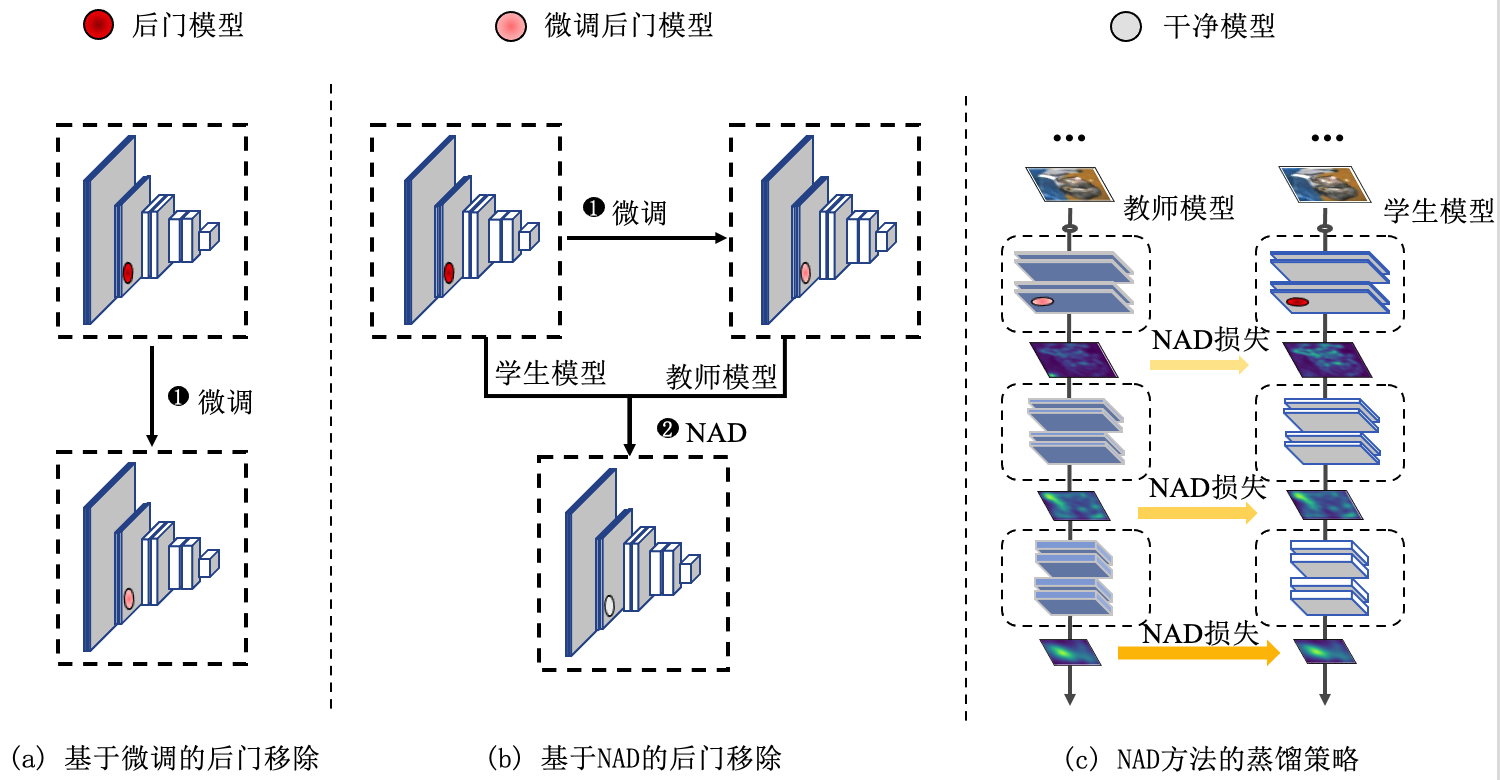
图9.3.1 基于微调的后门移除与NAD后门移除 (Li et al., 2021)

对于注意力表征，假定模型第\(l\)层的输出特征表示为\(f^{l} \in \mathbb{R}^{C\times H \times W}\)，注意力表征函数\(A: \mathbb{R}^{C\times H \times W} \rightarrow \mathbb{R}^{H \times W}\)的目标是将模型输出的三维特征\(f^{l}\)沿通道维度进行融合。具体来说，算子\(A\)有三种选择：

(9.3.8)\[A_{\text{sum}}\left(f^{l}\right)=\sum_{i=1}^{C}\left|F_{i}^{l}\right| ; A_{\text{sum}}^{p}\left(f^{l}\right)=\sum_{i=1}^{C}\left|F_{i}^{l}\right|^{p} ; A_{\text {mean }}^{p}\left(f^{l}\right)=\frac{1}{c} \sum_{i=1}^{C}\left|F_{i}^{l}\right|^{p},\]

其中，\(f_i^l\)表示第\(i\)个通道的激活图；\(A_{\text{sum}}\)对应整个激活区域，既包括良性也包括后门神经元的激活区域；\(A_{\text{sum}}^p\)是\(A_{\text{sum}}\)的一个幂次变换，目标是放大后门神经元和良性神经元之间的差异；\(A_{\text{mean}}^{p}\)计算所有激活区域的平均值，目的是将后门神经元的激活中心与良性神经元的激活中心（均值）对齐。

为了实现注意力的有效蒸馏和后门移除，Li等人将教师和学生模型之间的第\(l\)层的蒸馏损失定义为：

(9.3.9)\[\mathcal{L}_{\text{NAD}}\left(f_T^{l}, f_S^{l}\right)=\left\|\frac{A\left(f_T^{l}\right)}{\left\|A\left(f_T^{l}\right)\right\|_{2}}-\frac{A\left(f_S^{l}\right)}{\left\|A\left(f_S^{l}\right)\right\|_{2}}\right\|_{2},\]

其中，\(\left\|\cdot\right\|_2\)表示\(L_2\)范数，用来衡量教师和学生注意力之间的距离。

NAD方法的整体优化损失函数由失交叉熵损失（\(\mathcal{L}_{\text{CE}}\)）和神经元注意蒸馏损失（\(\mathcal{L}_{\text{NAD}}\)）两部分组成：

(9.3.10)\[\mathcal{L}=\mathbb{E}_{( x, y) \sim D_c}\left[\mathcal{L}_{\text{CE}}\left(f_S( x), y\right)+\beta \cdot \sum_{l=1}^{K} \mathcal{L}_{\text{NAD}}\left(f_T^{l}( x), f_S^{l}( x)\right)\right],\]

其中，\(\mathcal{L}_{\text{CE}}\)衡量学生模型的分类误差，\(D_c\)是用来干净防御数据集，\(l\)代表残差网络层的索引，\(\beta\)是用来控制蒸馏强度的超参数。

NAD后门防御开启了基于知识蒸馏技术的双模型相互纠正防御思路，是目前业界比较简单有效的方法之一，能够抵御大多数已知的后门攻击。但是该方法面对更新更强的攻击时还存在不小的局限性，毕竟以在防御数据上微调过一次的后门模型作为教师模型并未完全发挥知识蒸馏的潜力。相信选择更优的教师模型会大大提高此类方法的有效性。

对抗神经元剪枝。 从后门模型中准确检测并隔离出后门神经元是后门防御领域的一个挑战性问题。Wu等人 (Wu and Wang, 2021) 提出了一种基于对抗神经元扰动的对抗神经元剪枝（adversarial neural perturbation, ANP ）方法，帮助缓解后门触发器对模型的负面影响。此工作研究发现，后门神经元（即后门模型中与后门功能相关的神经元）在参数空间的对抗扰动下更容易崩溃，从而导致后门模型在干净样本上预测后门标签。基于此发现，作者提出一种新颖的对抗模型剪枝方法，该方法通过剪枝一些对对抗噪声敏感的神经元来净化后门模型。实验表明，即使只借助1%的干净样本，ANP也能有效地去除模型后门，且不会显著影响模型的原始性能。

ANP防御方法主要包含三个步骤：参数对抗扰动、剪枝掩码优化和后门神经元裁剪。给定一个训练完成的模型\(f\)，对应的模型权重表示为\(w\)，干净训练样本子集表示为\(D_{c}\)以及交叉熵损失函数表示为\(\mathcal{L}_{\text{CE}}\)。针对模型参数空间的对抗扰动可定义如下：

(9.3.11)\[\max_{\delta, \mathbf xi \in [- \epsilon, \epsilon]}\mathbb{E}_{D_{c}} \mathcal{L}_{\text{CE}} \left((1+\delta) \odot w, (1+\mathbf xi) \odot b \right),\]

其中，\(\epsilon\)用于控制对抗扰动的大小，\(\delta\)和\(\mathbf xi\)分别代表添加在权重\(w\)和偏置项\(b\)上的对抗噪声。

为了实现精准剪枝，ANP定义了一个模型参数空间上的连续掩码\(m \in [0,1]^{n}\)，初始化值为1，并且使用投影梯度下降法（即PGD对抗攻击）对\(m\)进行更新。为了减小神经元裁剪对模型干净准确率的负面影响，ANP在参数扰动的同时也在干净样本上使用交叉熵对模型进行微调。为此，作者定义了以下优化目标函数：

(9.3.12)\[\min_{ m \in[0,1]^{n}} \mathbb{E}_{D_c}\left[\alpha \mathcal{L}_{\text{CE}}( m \odot w, b)+(1-\alpha) \max _{\delta, \boldsymbol{\mathbf xi} \in[- \epsilon, \epsilon]^{n}} \mathcal{L}_{\text{CE}}(( m+\boldsymbol{\delta}) \odot w,(1+\boldsymbol{\mathbf xi}) \odot b)\right]\]

其中，\(\alpha \in [0,1]\)为平衡系数。当\(\alpha\)接近1时，更关注裁剪后的模型在干净数据上的准确率，而当\(\alpha\)接近0时，更关注后门的移除效果。

需要注意的是，上式优化得到的掩码\(m\)记录了神经元在对抗噪声下的敏感程度。为了有效移除模型中的后门神经元，可以对优化得到的\(m\)，基于预先设定的裁剪阈值\(T\)，将所有小于阈值的神经元的权重置为0。 实验表明，ANP在多种后门攻击上都取得了最佳的防御效果。但是，ANP对于特征空间的后门攻击方法仍然存在一定的局限性。神经元裁剪是一种极其高效的后门防御方法，有必要持续探索更先进的裁剪方法，对关键的后门神经元进行精准定位和移除。

9.4. 本章小结

本章介绍了针对后门攻击的防御方法。其中，章节 9.1节 介绍了检测一个模型是否是后门模型的方法，后门模型往往在后门类别上表现出非常规的性能，比如决策边界靠近其他类别、可以被逆向出后门触发器等。章节 9.2节 介绍了检测一个样本是否是后门样本的方法，可以通过分析样本在特征分布方面的异常来完成。章节 9.3节 介绍了研究最多的一种后门防御策略，即后门移除，此类方法通过借助一小部分干净数据结合微调、剪枝、蒸馏等技术，将后门神经元从模型中清除，还原一个纯净无后门的模型。综合来看，基于剪枝的后门防御方法在简便性、高效性和实用性方面占据一定的优势，未来具有在大规模预训练模型上应用的可能。另外，基于鲁棒训练的后门防御方法，比如能够同时应对噪声标签、损坏输入以及投毒数据的鲁棒训练框架，具有在更广泛的场景下应用的可能。