7. 模型安全:对抗防御¶
针对对抗攻击的防御工作主要集中在三个方面。首先是对抗样本成因研究,正所谓“知己知彼,百战不殆”,只有深入了解对抗样本的成因,才能设计防御方法从源头上防御住对抗攻击。其次是对抗样本检测,检测是一种便捷的防御,其不光能让防御者对检测出来的攻击拒绝服务,而且还能通过检测到的查询样本定位到攻击者,从而对其进行及时的提醒和警告。第三是对抗训练,这是一种主流的对抗防御手段,其通过鲁棒优化的思想在训练过程中提高模型自身的鲁棒性。其他的防御策略还包括输入空间防御、可认证性防御等。下面将对这些防御策略进行详细介绍。
7.1. 对抗样本成因¶
理解对抗样本存在的根本原因有助于设计更有效的防御策略。自2013年对抗样本发现以来,研究者已经提出了多种对抗样本成因假说,解释对抗样本的一些独有性质。但是关于对抗样本的成因,领域内目前并没有达成一致的结论,有时不同的假说之间也存在一定的冲突。
直观来讲,对抗样本是针对模型的攻击,而模型又可以从不同的角度去理解,即学习器、计算器、存储器、复杂函数等,同时模型具有特征空间、决策边界等不同组成部分,导致对抗样本的成因可以从多种角度来解释。下面将介绍几个经典的假说,包括高度非线性假说、局部线性假说、(决策)边界倾斜假说、高维流形假说和不鲁棒特征假说。这些假说都是基于深度学习模型提出的。
7.1.1. 高度非线性假说¶
通常,我们认为一个良好的模型应当具备很好的泛化能力,而泛化能力又分为非局部泛化(non-local generalization)和局部泛化(local generalization)。非局部泛化能力是指模型能够为不包含训练样本的邻域分配正确的概率。例如,同一个物体在不同视角下的图片从像素层面来看差异较大,在向量空间中距离较远,但实际上二者具有相同的语义标签,在这种情况下如果模型能够正确分类两张图片,则称其具备一定的非局部泛化能力。而局部泛化能力则强调模型的平滑性,要求模型能够在靠近训练样本的测试样本上也能够按照预期工作。具体来说,对于给定的训练样本\(x\),设定足够小的球半径约束\(\epsilon\),如果模型能对以\(x\)为中心、\(\epsilon\)为半径的高维球\(\mathcal{B}_{ \epsilon}( x)\)内的所有样本都给出类似的预测结果,则模型具有局部泛化能力。 Yoshua Bengio在2009年作出了基于核方法的平滑假说 (Bengio and others, 2009) ,认为模型的局部泛化能力往往强于非局部泛化能力。其中,弱非局部泛化能力体现在:模型会将一些不重要的概率分配给输入空间中未被训练样本覆盖的区域,而这些区域可能表示与训练数据相同的物体;而强局部泛化能力则体现在模型对输入数据上的微小随机扰动不敏感。
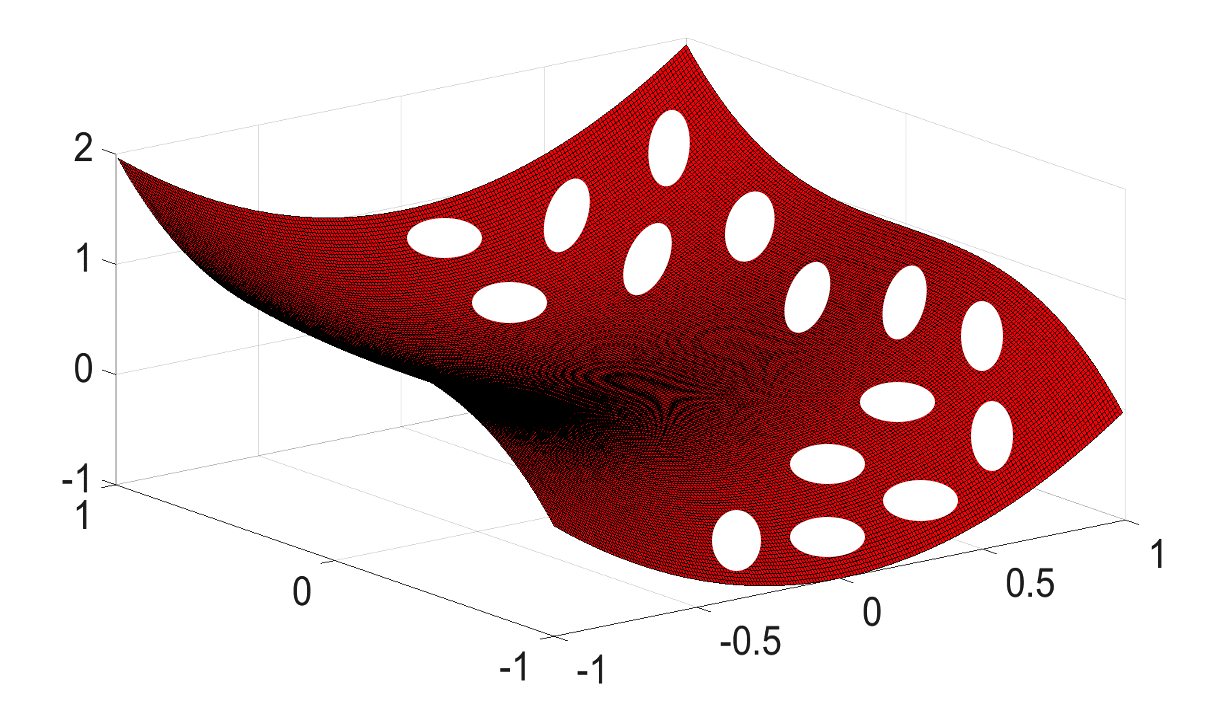
图7.1.1 深度神经网络所学到的数据流形(红色曲面)附近存在大量低概率对抗“口袋”(白色空洞) (Szegedy et al., 2014)¶
Szegedy等人 (Szegedy et al., 2014) 则认为上述平滑假说对高度非线性的神经网络并不成立。为了支撑这一观点,他们以图像输入为例提出了一套能够在输入样本邻域中寻找对抗样本的算法(即章节 6.1节 介绍的L-BFGS算法),通过对抗样本来构造局部泛化的反例。实验表明,随机噪声确实难以产生对抗样本,但通过对抗算法几乎可以为每一个输入样本找到微小的对抗扰动,使模型对扰动后的样本错误分类,证明了神经网络的弱局部泛化。Szegedy等人对此做出猜想:正常情况下,对立否定集(对抗样本集)出现的概率极低,因而很少出现在测试集中,但它是密集的(很像有理数),因此几乎在每个测试用例中都能被找到。
为什么会存在对抗样本呢?为了回答这个问题,Szegedy等人进一步提出了高度非线性假说,认为对抗样本的存在是由高度非线性化导致的局部泛化缺陷。具体来说,深度神经网络具有高维特征空间,同时非线性激活和层间堆叠导致输入和输出之间的映射高度非线性化,导致高维空间中存在大量未被探索过的“高维口袋”(high-dimensional pockets)。这些“高维口袋”无法被普通样本覆盖到,所以未经过充分训练(受有限训练样本限制),其内部的类别信息无法预测(即口袋中的样本类别不确定)。普通样本很容易沿着对抗方向(通过添加对抗噪声的方式)进入“高维口袋”,使模型发生预测错误。此外,这些“高维口袋”可能是大量存在的,即对抗子空间可能会占据特征空间的很大一部分。
虽然高度非线性假说很直观的解释了对抗样本的成因,但其还存在大量的遗留问题。比如,对抗子空间存在的形式,是否是每个样本周围都会存在对抗子空间;对抗子空间是如何在模型训练的过程中形成的,跟决策边界有什么关系;普通测试样本为什么很难到达对抗子空间;对抗子空间是否可以通过采样或者数据增广弥补等。回答这些问题需要更深入、更广泛的研究,因为在一个或者一种模型上得到的结论可能并不能代表所有模型。
7.1.2. 局部线性假说¶
深度神经网络实际上包含很多(接近)线性的操作,比如LSTM网络 (Hochreiter and Schmidhuber, 1997) 、ReLU激活函数 (Glorot et al., 2011, Jarrett et al., 2009) 和Maxout网络 (Goodfellow et al., 2013) 等都以非常线性的方式运行。而这种局部线性性质很可能是对抗样本存在的原因。受此启发,Goodfellow等人 (Goodfellow et al., 2015) 提出局部线性假说,认为对抗样本是深度神经网络局部线性化的必然产物。局部线性假说的核心思想是:尽管深度神经网络整体呈非线性,但其内部存在大量局部线性操作,基于局部线性性质进行攻击足以产生对抗样本。
局部线性假说的认证思路如下:首先以线性模型为例展示高维线性转换对输入变化的无限放大,然后基于深度神经网络中存在的线性行为设计线性对抗攻击算法,最后通过实验认证“深度神经网络的线性化导致对抗样本存在”的合理性。
给定一个线性模型\(f(x)=w^{\top}x+b\),假设给输入添加的扰动噪声为\(\mathbf{\delta}=sign(w)\cdot\epsilon\),其中\(sign(\cdot)\)是符号函数,\(\epsilon>0\)是每个输入维度上的扰动大小,则模型在扰动前后的输出变化为:
其中,\(n\)表示线性模型参数的维度。从上式可以看出,模型的输出变化随参数的维度增加而增加,即当参数维度(也即输入维度)趋向于正无穷的时候,模型输出变化也趋向于正无穷,即\(\lim_{n\rightarrow +\infty} \Delta f = +\infty\)。而深度神经网络的参数维度很高,所以如果局部线性性质是对抗样本的成因,那么线性的攻击方法就足以为几乎每一个样本找到对抗样本。
实验表明,基于Goodfellow等人提出的线性攻击方法FGSM(参考章节 6.1节 )确实能够达到较高的攻击成功率。在\(\epsilon=0.25\)的无穷范数(\(L_{\infty}\))约束下,FGSM攻击可以让浅层softmax分类器在MNIST测试集上的错误率达到99.9%,平均置信度为79.3%;在同样的参数设置下,攻击使Maxout网络在MNIST测试集上的错误率达到了89.4%,平均置信度高达97.6%。类似的,当使用\(\epsilon=0.1\)时,卷积Maxout网络在CIFAR-10测试集上的错误率高达87.15%,平均置信度高达96.6%。这说明基于线性假说生成的对抗扰动能够在非线性神经网络上取得非常好的攻击效果,支持了局部线性化是对抗样本成因的结论。
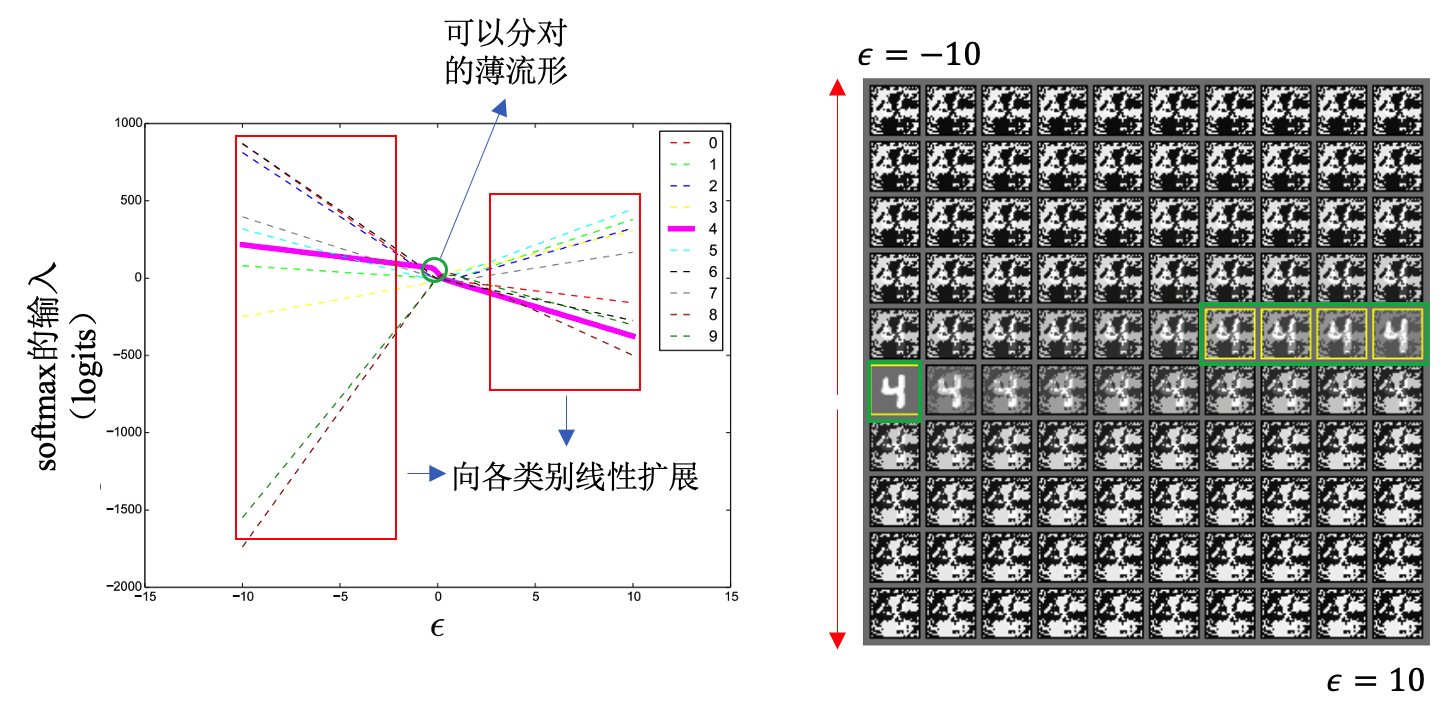
图7.1.2 左图:给定一个MNIST样本(中心点),沿着FGSM算法找到的对抗方向,向\(\epsilon=10\)和\(\epsilon=-10\)两个方向逐步增加噪声,神经网络的逻辑值(logits)发生线性变化,同时能正确分类的部分(绿色圆圈)很小(流形很薄)。右图:对应左图中变化\(\epsilon\)所得到的对抗样本。图片来自 (Goodfellow et al., 2015) 。¶
基于局部线性假说,Goodfellow等人进一步解释了对抗样本的跨模型迁移性。如图 图7.1.2 所示,从某一个样本出发沿着FGSM找到的对抗方向不断增加扰动时,模型对应不同类别的逻辑值发生线性的变化,同时能保持正确分类的部分(左图中的绿色圆圈部分)很小,也就是说正确的流形实际上很薄,流形外是巨大的对抗子空间。这导致了不同模型虽然在所学到的流形上有一定的差别,而在对抗子空间上存在大量重叠,这也解释了对抗样本的扩模型迁移性。
7.1.3. 边界倾斜假说¶
Tanay和Griffin (Tanay and Griffin, 2016) 对局部线性假说提出了疑问,并设计了两个可以否定局部线性假说的例子。按照局部线性假说,模型的对抗脆弱性会随着输入维度和模型参数维度的增加而加重。针对这个解释,Tanay和Griffin基于MNIST数据集中的两类手写体数字3和7,设计了两个对比数据集:(1)原始大小(\(28\times 28\))的数字3和7;(2)放大(\(200\times 200\))了的数字3和7。Tanay和Griffin展示了模型在这两个数据集上的对抗样本现象并未(明显)加重。需要注意的是Tanay和Griffin的实验使用的是线性SVM模型和\(L_2\)范数攻击,而Goodfellow等人的实验使用的是逻辑回归模型和\(L_{\infty}\)范数攻击。这个实验从一定程度上挑战了Goodfellow等人的线性解释,即输入维度的增加并没有加重对抗脆弱性。
紧接着,Tanay和Griffin构造了一个不存在对抗样本的分类任务,来证明并不是所有的线性分类问题都会存在对抗样本现象。这个分类任务是这么构造的,考虑一个图像二分类问题,两类图像的大小是\(100\times 100\),类别1的图像是左半边为\([0,1]\)之间的随机像素值,右半边是纯黑像素(像素值全为0),类别2的图像是左半边为\([0,1]\)之间的随机像素值,右半边是纯百像素(像素值全为1)。对于上述分类问题,通过FGSM算法生成的对抗样本只能是在将类别1的图像完全转换成类别2的图像时才能成功攻击,反之亦然。所以上述分类问题并不存在对抗样本,从而挑战了Goodfellow等人的线性解释,即线性分类器沿着对抗方向扰动一定会得到一个对抗样本。
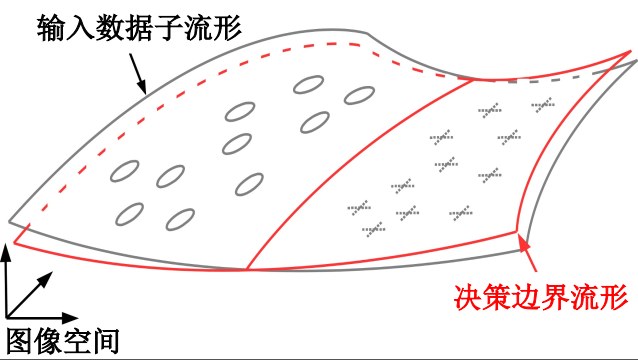
图7.1.3 决策边界倾斜导致其与数据流形之间发生了偏差,导致对抗样本的存在 (Tanay and Griffin, 2016) 。¶
受启发于Szegedy等人的高维非线性假说,Tanay等人提出了边界倾斜假说,即模型学习到的决策边界与数据的潜在流形存在轻微的倾斜偏离(如图 图7.1.3 所示),导致二者之间的间隙空间存在对抗样本,即样本可以跨过决策边界但是语义内容仍然在流形附近。决策边界倾斜假说很好的解释了对抗样本两个主要性质:(1)对抗样本可以让模型犯错,即跨过了决策边界;(2)对抗样本跟原始样本极为相似,即对抗样本仍然在原始样本附近的流行上。边界倾斜假说与高维非线性假说并不冲突,高维非线性空间中决策边界和数据流形更为复杂,两者之间的偏离空间更加复杂。可惜的是,目前并不存在能有效可视化决策边界或者流形的方法,导致我们无法看到二者的真实形态。
7.1.4. 高维流形假说¶
Ma等人 (Ma et al., 2018) 提出高维流形假说,认为对抗样本周围子空间(即对抗子空间)对应流形的本质维度(intrinsic dimensionality)更高,即对抗样本从低维流行跃迁到了高维流形。此解释基于机器学习的“流形假说”,即真实世界中的高维数据往往对应一个低维流形。此外,高维流形假说跟Szegedy等人的高维非线性假说也是一脉相承的,只不过这里计算出了具体的高维维度(即本质维度)。图 图7.1.4 展示了高维流形假说中普通样本和对抗样本周围子空间的本质维度,其中对抗子空间的维度远高于普通子空间。
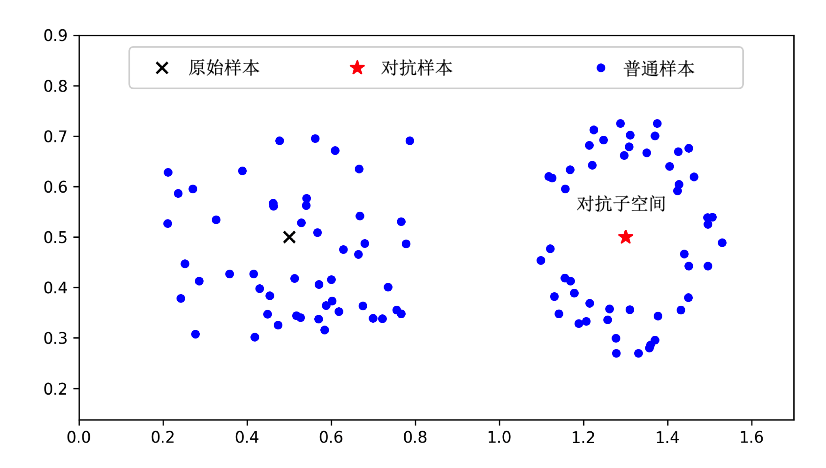
图7.1.4 对抗样本处在更高维的子空间里 (Ma et al., 2018) 。左边普通样本周围子空间的本质维度为1.53,右边对抗样本周围子空间的本质维度为4.36。¶
本质维度的概念在流形学习、特征降维、异常检测等领域已有大量研究。比如在特征降维研究中,本质维度可以告诉我们数据到底可以降到多少维。本质维度可以从全局和局部两个不同角度研究,全局本质维度衡量的是整个数据集的维度,而局部本质维度衡量的是一个样本周围子空间的本质维度。在高维流行假说中,Ma等人使用局部本质维度对对抗样本周围的子空间进行了维度测量。以欧式空间为例,两个\(m\)-维球体的体积与半径之间的关系可以告诉我们整个空间的维度:
其中,\(V_1\)和\(V_2\)是两个球体的体积,\(r_1\)和\(r_2\)是两个球体的半径。将此概念迁移到统计意义上的连续距离分布,即可得到局部本质维度(local intrinsic dimensionality,LID)的正式定义:
定义
类比之前欧式空间的例子,这里累积分布函数\(F(r)\)相当于是体积,而样本\(x\)到其他样本的距离\(r\)为半径。由于我们并不知道\(F(r)\),所以需要基于一定的假设对样本\(x\)的LID值进行估计,比如假设\(x\)的\(k\)-近邻距离分布符合广义帕累托分布(generalized Pareto distribution,GPD)。一个经典的估计方法是下面的最大似然估计(maximum likelihood estimate,MLE)方法 (Amsaleg et al., 2015) :
其中,\(r_i( x)\)是\(x\)到其第\(i\)个邻居样本的距离,\(k\)表示\(x\)的\(k\)-近邻样本。
基于上述LID估计方法,Ma等人展示了对抗样本的LID值比普通样本或添加了随机噪声的样本都要高,即对抗子空间的本质维度明显高于其他样本。Ma等人进一步展示了样本的LID特征可以用来训练对抗样本检测器,在不同攻击上都表现出了不错的检测结果。与高维非线性假说不同,高维流形假说研究的是特征空间的本质维度并不是它的表示维度(representation dimension)。从本质维度的角度来说,Tanay等人反驳局部线性假说的两个反例都是可以解释的,第一个反例(即将输入图像等比变大并不会导致更严重对抗脆弱性)中本质维度在图像放大前后保持不变,所以对抗脆弱性也就相同;第二个反例中的二分类问题的本质维度为1,而一维空间不存在对抗样本也是合理的。
7.1.5. 不鲁棒特征假说¶
对抗样本通常很难被人眼察觉,亦即人眼对对抗扰动噪声并不敏感,从这个角度来讲,人类“看得见”的特征可以被粗略的理解为“鲁棒特征”。而对于神经网络来说,很多人类“看得见”的特征(如“尾巴”、“耳朵”等)并不比其他隐蔽的特征更具有结果预测性。以图像分类为例,模型在学习过程中会最小化分类错误,利用一切可以利用的分类信号进行学习,这其中往往包括人类无法理解的不鲁棒特征。Ilyas等人 (Ilyas et al., 2019) 将模型学习的对结果预测有用的特征定义为有用特征(useful features),并提出有用特征可以是鲁棒的也可以是不鲁棒的,其中鲁不鲁棒是由微小噪声对模型输出改变的多少来定义的。
给定一个二分类问题(\(\mathcal{Y} = \{+1, -1\}\)),基于从分布\(\mathcal{D}\)中采样得到的“输入-标签”对\(( x,y)\in \mathcal{X} \times \mathcal{Y}\)来训练一个分类器,使其具备正确将输入映射到标签的能力\(C:\mathcal{X} \rightarrow \{±1\}\)。 使用符号\(\mathcal{F}\)表示所有特征的集合,定义为\(\mathcal{F}=\{f: \mathcal{X} \rightarrow \mathbb{R} \}\),其中\(f( x)\)表示将输入空间映射到实数空间的特征函数。假定\(\mathcal{F}\)中的所有特征函数都经过了零均值化和单位方差归一化,即满足\(\mathbb{E}_{( x,y)\in\mathcal{D}}[f( x)]=0\)且\(\mathbb{E}_{( x,y)\in\mathcal{D}}[f( x)^2]=1\),从而让后续定义具有尺度不变性。基于此,Ilyas等人 (Ilyas et al., 2019) 定义 了\(\rho\)-useful特征、\(\gamma\)-robustly useful特征和useful, non-robust特征。
\(\rho\)-useful特征: 对于给定数据分布\(\mathcal{D}\),当特征\(f\)满足公式 (7.1.5) 时称其为\(\rho\)-useful特征(\(\rho > 0\)),即特征与标签乘积的期望值不小于某个正数。
基于此,可以定义\(\rho_{\mathcal{D}}(f)\)为数据分布\(\mathcal{D}\)(所有样本)上特征\(f\)满足\(\rho\)-useful特性的最大的\(\rho\),它表示特征\(f\)在整个分布上的“有用性”。
\(\gamma\)-robustly useful特征:假定已经拥有了一个\(\rho\)-useful特征\(f\)及其在\(\mathcal{D}\)分布上的\(\rho_\mathcal{D}(f)\),对输入样本\(x\)及其\(\Delta\)邻域中的所有数据点,计算\(y\cdot f(x+\delta)\)的最小值作为下确界\(\mathop{\text{inf}}_{\delta \in \Delta( x)} y \cdot f(x+\delta)\),如果下确界在分布\(\mathcal{D}\)上的期望大于某个正数\(\gamma\)(\(0<\gamma\leq \rho\)),即满足公式 (7.1.6) ,那么称这样的特征是\(\gamma\)-robustly useful特征。
\(\gamma\)-robustly useful特征是指在一定领域内最坏扰动情况下仍能保持\(\gamma\)有用性的特征,也就是对分类有用且鲁棒的特征。
Useful, non-robust特征: 延续上述定义形式,定义另一类特征为“有用但不鲁棒”特征,一方面特征\(f\)是\(\rho\)-useful特征,另一方面它又不属于\(\gamma\)-robust特征,那么这样的特征对对抗噪声敏感,容易因对抗扰动而发生预测错误,所以有用但不鲁棒。
基于上述定义,Ilyas等人基于分类任务进行实验,以“对抗训练得到的模型倾向于使用鲁棒特征”为前提,通过解耦鲁棒特征和非鲁棒特征的方式来证明真实数据集中广泛存在有用但不鲁棒特征,是导致对抗样本出现的原因。 具体来说,先通过对抗训练 (Madry et al., 2018) 获得一个(在一定程度上)鲁棒的模型和一个普通训练的不鲁棒模型,然后通过蒸馏+数据扰动的方式,对原始数据集进行扰动得到两个版本(即只包含鲁棒特征的鲁棒数据集:math:`D_{R}`和只包含不鲁棒特征的不鲁棒数据集\(D_{NR}\))。下面介绍基于原始数据集\(D\)构造鲁棒和不鲁棒数据集的方法。
给定一个在\(D\)上普通训练的模型\(f\)(不鲁棒模型)和对抗训练的鲁棒模型\(f_R\),对\(D\)中的每个样本\(x\)进行如下变换可以得到鲁棒数据集\(D_R\):
其中,\(f_R\)取其特征层(比如最后一层卷积的输出),\(x'\)为与\(x\)随机配对的另一个样本,扰动得到的鲁棒样本\(x_R\)会被标记为类别\(y\)并添加到鲁棒数据集\(D_R\)中。公式 (7.1.7) 通过将\(x'\)的特征借助鲁棒模型\(f_R\))“鲁棒”的变为\(x\)的特征,在此过程中将\(x'\)中的不鲁棒特征移除。式 (7.1.7) 可由归一化的梯度下降(normalized gradient descent)求解。
通过下面的转换可以得到不鲁棒版本的\(x\):
其中,\(\mathcal{L}_{\text{CE}}\)为交叉熵损失函数,\(t\)为对抗目标类别(比如真实类别\(y\)的下一个类别\(y+1\)),\(\epsilon\)为\(L_2\)范数下的最大扰动上限。公式 (7.1.8) 可由基于\(L_2\)范数的PGD攻击算法求解。
实验表明,在\(D_{R}\) 上普通训练的模型具有天然鲁棒性,而在\(D_{NR}\)上普通训练的模型相比在原始数据集\(D\)上训练具有更差的鲁棒性,但是这些特征足够让模型获得不错的预测性能。这也说明了,同样都是高预测性特征,两类特征的鲁棒性存在巨大差别,而对抗样本的存在与模型使用了不鲁棒性特征有关。
更有意思的是,对抗样本的跨模型迁移性说明不同模型会学习类似的不鲁棒特征。这引发了三个发人深思的问题:1)不鲁棒特征是否是深度学习成功的秘诀?2)不鲁棒特征到底是什么?3)为什么不鲁棒特征比人类视角的鲁棒特征更具有结果预测性?这三个问题的答案或许能解开深度学习的黑箱。
关于对抗样本的成因还存在一些其他方面的假说。比如,“数据不足假说”认为训练数据的不足导致无法训练鲁棒的模型,而训练鲁棒的模型至少需要\(\mathcal{O}(\sqrt{d})\)(\(d\)是输入维度)个样本 (Schmidt et al., 2018) 。此假说的理论分析是基于高斯分布和线性分类器进行的,而实际上训练一个鲁棒模型所需要的样本数可能远远不止\(\mathcal{O}(\sqrt{d})\)。Fawzi等人 (Fawzi et al., 2016) 以及Gilmer等人 (Gilmer et al., 2019) 认为对抗样本是噪声带来的测试错误,因为某些随机噪声也可以导致模型发生较大的预测错误,并建议将对抗样本的研究跟普通图像损坏(common corruption)一起研究。而实际证明,通过向输入中添加随机噪声的训练方式也确实能让模型获得一定的鲁棒性 (Cohen et al., 2019) 。虽然关于对抗样本存在的根本原因目前尚无定论,但是对抗样本的存在从侧面说明了当前深度学习模型尚未达到真正亦或鲁棒的智能。
7.2. 对抗样本检测¶
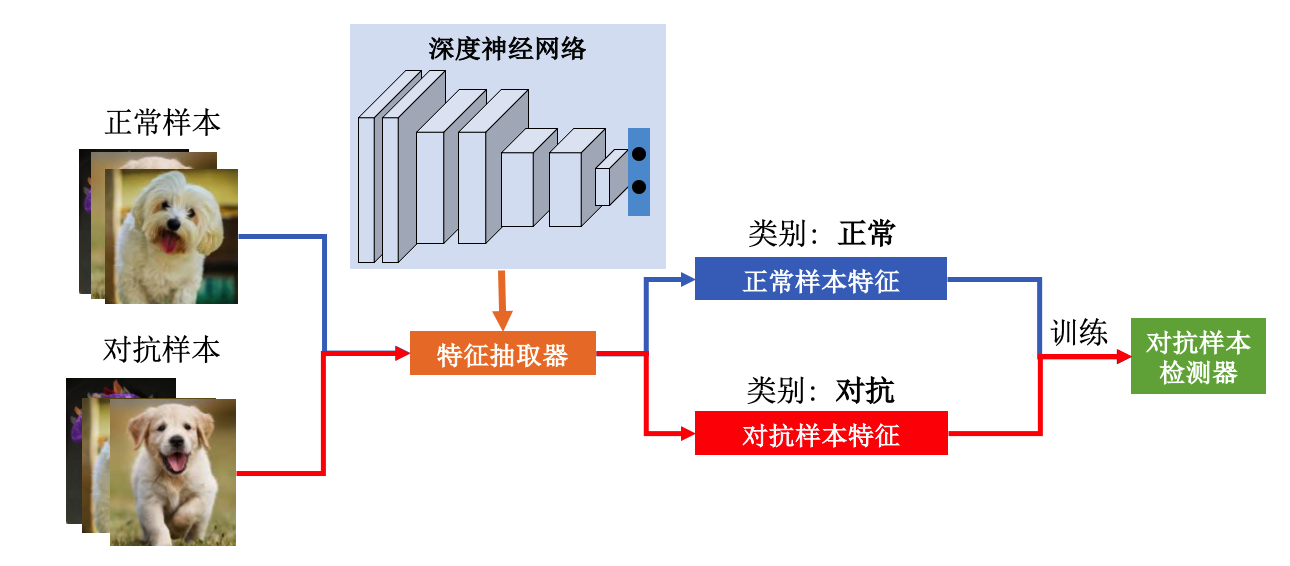
图7.2.1 对抗样本检测器的一般训练流程¶
对抗样本检测(adversarial example detection,AED)是一种很直接也很实用的对抗防御策略,在实际应用场景下可以检测对抗攻击并拒绝服务。图 图7.2.1 展示了训练一个对抗样本检测器的一般流程。对抗样本检测任务本身是一个二分类问题,检测器需要对输入进行“正常”还是“对抗”的判别。我们可以收集一定数量的正常样本和其对应的对抗样本,然后基于要保护的模型\(f\)抽取不同类型的特征,比如中间层特征、激活分布等。最后将两类样本的特征标记为“正常”和“对抗”类别,组成对抗检测训练数据集\(D_{\textup{train}}\)。我们可以在\(D_{\textup{train}}\)上训练一个任意的分类模型作为最终的检测器\(g\)。在测试阶段,我们先将待检测的样本送入模型\(f\)抽取特征,然后以抽取的特征为检测器\(g\)的输入进行检测。
在介绍具体的检测方法之前,我们先来分析一下对抗样本检测任务本身的一些特点。
对抗样本检测是异常检测(anomaly detection)的一个特例,只不过这里“异常”的是对抗样本。所以任何异常检测的方法都可以用来检测对抗样本。
对抗样本检测的关键是特征提取,特征的好坏直接决定了检测器的性能。这里会产生一个疑问:“为什么不能把正常和对抗样本直接输入检测模型,让模型自己去学习检测”?相关实验表明这种方式效果并不好,有两个可能的原因:(1)对抗噪声也是一种特征,导致对抗样本与正常样本在输入空间并没有区分度;(2)容易过拟合到有限类型的训练对抗样本,导致训练得到的检测器泛化性差。不过端到端的检测器训练方式还是值得探索的,尤其是在推理阶段与原始模型\(f\)的融合。
训练对抗样本的多样性决定了检测器的泛化能力,所以训练一个高性能的检测器往往需要尽可能多的利用不用类型的对抗样本来训练。
对抗样本检测器也是一种模型,它本身也会收到对抗攻击,而且往往都不鲁棒 (Carlini and Wagner, 2017) 。如何训练一个对抗鲁棒的检测器仍是一个探索中的问题。
对抗样本检测需要检测所有已知攻击和未知攻击,需要非常强的泛化能力,是一个巨大的挑战。很多检测器只能检测一些特定类别的对抗样本,或者某些特定参数下生成的对抗样本。如何训练更通用的对抗样本检测器是构建检测防御的首要任务。
以检测为中心的防御实际上是一种实用性极高的对抗防御策略。对抗样本检测脱离于模型的训练与部署之外,对模型不会产生任何干预,而且训练和推理效率往往很高。此外,可以训练多个检测器应对复杂多变的对抗攻击,检测结果还可以作为证据对攻击者发起追责。
下面介绍六大类经典的对抗样本检测方法。这些方法的分类参照了2017年Carlini和Wagner对10种典型对抗样本检测方法的测试评估工作 (Carlini and Wagner, 2017) 。具体类别包括:二级分类法、主成分分析法、异常分布检测法、预测不一致性、重建不一致性和诱捕检测法。
7.2.1. 二级分类法¶
二级分类法为对抗样本定义一个新的类别,然后利用原模型(要保护的模型)、增加检测分支、增加新检测模型等方式来训练对抗样本检测器。相对于原分类任务来说,对抗样本检测是一个二级分类任务,所以我们将此类方法称为二级分类法。代表性的工作包括Grosse等人提出的对抗重训练(adversarial retraining) (Grosse et al., 2017) 、Gong等人提出的对抗分类法 (Gong et al., 2017) 、以及Metzen等人提出的级联分类器(cascade classifier) (Metzen et al., 2017) 等。这些检测方法的思想比较类似:先普通训练一个分类器,然后对其生成对抗样本,那么生成的对抗样本一定具有独特的性质可以自成一类。二级分类法在检测流程上也比较类似。
对抗重训练。 Grosse等人提出的对抗重训练方法包括以下四步:
在正常训练集\(D_{\textup{train}}\)上训练得到模型\(f\);
基于\(D_{\textup{train}}\)对抗攻击模型\(f\)得到对抗样本集\(D_{\textup{adv}}\);
将\(D_{\textup{adv}}\)中的所有样本标注为\(C+1\)类别;
在\(D_{\textup{train}} \cup D_{\textup{adv}}\)上训练得到\(f_{\textup{secure}}\)。
与对抗重训练方法不同,在第三步里,Gong等人的对抗分类法将\(D_{\textup{train}}\)中的样本标注为类别0,将\(D_{\textup{adv}}\)中的样本标注为类别1,在第四步里训练一个二分类对抗样本检测模型\(g\)(比模型\(f\)更小)。Carlini和Wagner的测试结果显示,这两种方法得到的检测器对对抗攻击(\(L_2\)范数C&W攻击)都不鲁棒,不管是白盒威胁模型下(攻击者知晓检测器的参数)还是灰盒威胁模型下(迁移攻击),与没有防御相差并不多。
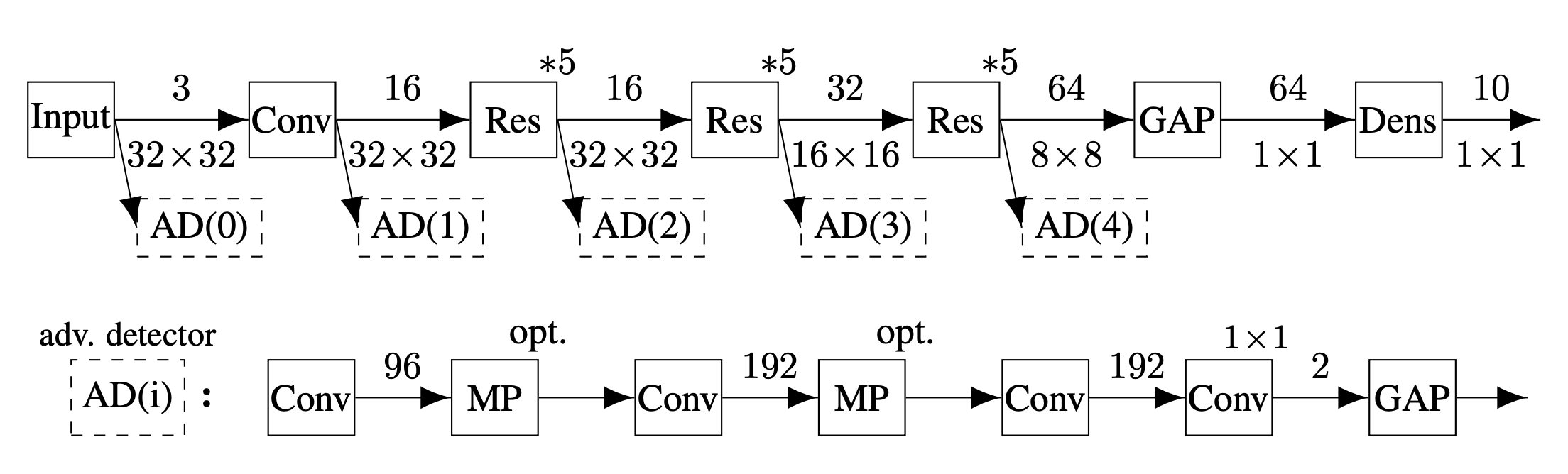
图7.2.2 基于级联分类器的对抗样本检测 (Metzen et al., 2017) (AD表示对抗样本分类器)¶
级联分类器。Metzen等人提出的级联分类器方法的训练步骤与Gong等人的对抗分类法类似,不同的是检测器的形式和训练方式。具体来说,级联分类器方法在神经网络的不同中间层,比如残差网络的每个残差块的输出部分,接上一个单独的检测器(0-1二分类器)。在训练级联检测器的时候,主模型\(f\)的参数是冻结的。为了应对动态多变的对抗攻击,比如专门针对检测器的白盒攻击,Metzen等人进一步提出在训练检测器的同时使用BIM攻击动态生成对抗样本,也就是检测器是对抗训练的 (Goodfellow et al., 2015) 。此方法虽然比前两个检测方法更鲁棒,但是依然无法防御更强的C&W攻击,在白盒和迁移攻击情况下都是如此。这主要是因为BIM对抗样本并不最有效的对抗训练样本,如果换成Madry等人后来提出的PGD攻击 (Madry et al., 2018) ,相信防御效果会有所提升。
实际上,基于开集(open-set)类别识别的开集网络(open-set networks)都可以用来识别对抗样本,即将对抗样本识别为未知类别。比如,Bendale等人 (Bendale and Boult, 2016) 提出的开集网络使用OpenMax层代替传统的Softmax层,以此来识别无关类别样本、愚弄样本(fooling example)或者对抗样本。结合对抗训练 (Madry et al., 2018) 的开集识别也是值得探索的对抗防御策略。
7.2.2. 主成分分析法¶
主成分分析(principle component analysis,PCA) (Wold et al., 1987) 是一种经典的数据分析和降维方法。PCA的思想是最大化投影后数据方差的同时最小化投影造成的损失。主成分是数据协方差矩阵(covariance matrix)的特征向量,可通过对数据的协方差矩阵做特征值分解(eigenvalue decomposition)或者直接对数据矩阵(data matrix)做奇异值分解(singular value decomposition,SVD)得到,其中一般通过后者实现。PCA可以直接用来分析对抗样本数据。总体来说,基于PCA的对抗样本分析与检测方法在对抗防御领域里只是昙花一现,因为PCA并不能在稍微复杂一点的数据集上发现对抗样本的不同之处。
PCA检测。Hendrycks和Gimpel (Hendrycks and Gimpel, 2016) 分析了对抗样本的主成分,并以此来检测对抗样本。具体来说,使用PCA白化(PCA whitening)对正常和对抗样本进行处理,白化所得样本的元素值对应PCA主成分的系数(比如第一个元素对应最大成分的系数)。在MNIST、CIFAR-10和Tiny-ImageNet数据集上的分析结果显示对抗样本在低排名成分(low-ranked components)的部分跟正常样本有明显区别。基于此,Hendrycks和Gimpel提出使用倒数几个成分的系数的方差进行对抗样本检测。然而, Carlini和Wagner的结果显示对抗样本的PCA只在MNIST数据集上有区别,在复杂数据集上并不成立 (Carlini and Wagner, 2017) 。而且对抗样本的小成分异常主要是由数据集本身的特点引起的,即MNIST手写体图片的背景是纯黑色的(像素值为0),所以微小扰动会让背景出现灰色像素(像素值不再为0),对图像的最后几个成分产生较大影响。所以主成分分析法受数据集本身特点的影响很大,一般很难在不同数据集上得到一致的结论,而且此类方法只是对输入样本进行分析并未考虑模型信息。
降维检测。说到PCA,我们就不得不提降维方法。Bhagoji等人提出使用PCA对输入数据进行降维,只使用最大的几个成分训练模型,以此来压缩对抗攻击的空间,提高模型的鲁棒性 (Bhagoji et al., 2017) 。Carlini和Wagner在MNIST数据集上的测试结果显示虽然降维确实可以提高鲁棒性,但是提升微不足道 (Carlini and Wagner, 2017) 。根据Goodfellow等人的线性假说和Simon等人对输入维度的分析 (Simon-Gabriel et al., 2019) ,降低输入维度有利于提高模型的对抗鲁棒性 (Goodfellow et al., 2015) ,但是这种自然鲁棒性在没有对抗训练加持的情况下收效甚微。
上述两个方法的失败说明只考虑输入空间的特性并不能准确检测对抗样本。Li和Li (Li and Li, 2017) 提出对神经网络的中间层结果进行PCA分析,并基于此设计了基于SVM的多级级联分类器进行对抗样本检测。在卷积神经网络上,对每个卷积层都接一个SVM分类器,在对应层PCA降维后的特征上训练。如果级联分类器中的任何一个检测器预测样本为对抗样本则判定其为对抗样本,如果所有的检测器都检测为正常样本才判定其为正常样本。此方法基于L-BFGS攻击在大数据集ImageNet上进行了实验认证,得到了不错的效果,但是Carlini和Wagner的测试发现其在小数据集MNIST和CIFAR-10上面对C&W攻击时效果欠佳。
7.2.3. 异常分布检测法¶
异常分布检测方法通过分析对抗样本或对抗特征的分布特点并使用统计指标来检测对抗样本,也可以基于计算出来的统计指标训练一个简单的分类器(如线性回归模型、SVM模型)执行最终的分类任务。对于异常分布检测方法来说最主要的是选择恰当的统计指标。此类方法是目前主流的对抗样本检测方法。
最大平均差异。Grosse等人 (Grosse et al., 2017) 提出使用最大平均差异(maximum mean discrepancy,MMD)来检测两个数据集(\(D_1\)vs.\(D_2\))是否来自于一个相同的数据分布,原假设(null hypothesis)为二者来自于相同分布。在假设已知\(D_1\)只包含正常样本的前提下,我们可以根据统计测试结果判定\(D_2\)是否为对抗样本集。为了应对数据的高维问题,Grosse等人采用了由Gretton等人提出的基于核的MMD测试 (Gretton et al., 2012) ,具体定义如下:
其中,上确界表示从核函数类\(\mathcal{K}\)中选择能最大化后面的函数差异的核函数\(k(\cdot)\),\(|D_1|=n\)和\(|D_2|=m\)表示两个数据集各自的样本数量。由于MMD无法直接计算,所以需要近似,Grosse等人采用了基于无偏MMD的渐近分布的测试 (Gretton et al., 2012) ,具体测试步骤如下:
在\(D_1\)和\(D_2\)上计算\(a=MMD(\mathcal{K},D_1,D_2)\);
对\(D_1\)和\(D_2\)中的样本顺序做随机打乱得到对应的\(D'_1\)和\(D'_2\);
在\(D'_1\)和\(D'_2\)上计算\(b=MMD(\mathcal{K},D'_1,D'_2)\);
如果\(a < b\)则拒绝原假设,即\(D_1\)和\(D_2\)来自不同分布;
重复执行步骤1-4很多次(1万次),计算原假设被拒绝的比例作为\(p\)-值。
在实验中,Grosse等人采用了高斯核函数(Gaussian kernel,也称径向基RBF)计算MMD,并在三个小数据集MNIST、DREBIN和MicroRNA上示了10-100个样本即可对对抗样本进行高置信度的区分且对抗扰动越大区分度越高。需要注意的是,MMD是计算在两个样本集合上的,不是对单个样本计算的,所以此方法无法检测单个样本。为了解决这个问题,Grosse等人采用了前面已经介绍的二级分类法 (Grosse et al., 2017) ,此方法独立于MMD统计测试。但是Carlini和Wagner的测试 (Carlini and Wagner, 2017) 发现这种方法依然无法在CIFAR-10数据集上检测C&W攻击。
核密度估计。Feinman等人 (Feinman et al., 2017) 提出核密度估计(kernel density estimation,KDE)方法来检测对抗样本。与MMD不同,KDE方法是作用在深度神经网络的逻辑输出(logits)上的(MMD是作用在输入空间上的)。给定一个被预测为类别\(t\)的样本\(x\),其KDE值的计算公式如下:
其中,\(X_t\)是类别\(t\)的训练样本子集,\(z\)表示模型最后一层的逻辑输出,\(\sigma\)是控制高斯核平滑度的带宽(bandwidth)超参,需要预先定义。基于KDE值,可以指定一个阈值\(\tau\),\(KDE( x) < \tau\)判定\(x\)为对抗样本,反之为正常样本,也可以直接在KDE值上训练一个简单的二分类器(如逻辑回归或SVM)作为对抗样本检测器。
KDE方法的出发点是对抗样本在深层空间会远离正常的数据流形,导致相对较低的核密度,主要受启发于Szegedy等人的高维非线性假说 (Szegedy et al., 2014) 。图 图7.2.3 展示了论文中列出的对抗样本在深度空间中的三种情况。从实际的实验结果来看这三种情况都有可能存在,因为基于KDE训练的检测器在不同数据集上并不稳定。Carlini和Wagner的测试结果显示,KDE在MNIST数据集上更好而在CIFAR-10数据集上则无法检测C&W攻击,且在MNIST可以被白盒适应性攻击 攻击掉(但是会显著增加成功攻击所需的扰动大小) (Carlini and Wagner, 2017) 。
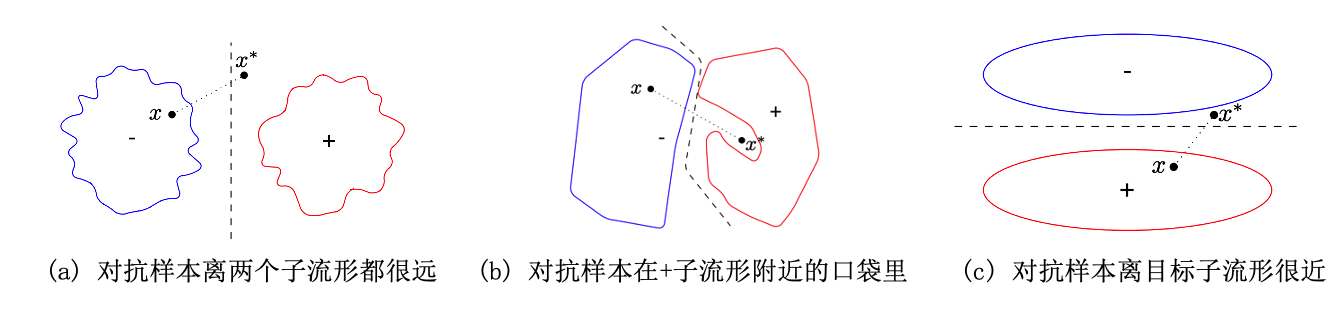
图7.2.3 KDE方法对数据流形和决策边界的三种假设 (Feinman et al., 2017) ,其中\(x^{*}\)为对抗样本,+/-表示两个子流形,虚线表示决策边界。¶
局部本质维度。结合高维流形假说,Ma等人提出使用局部本质维度(LID)指标来检测对抗样本 (Ma et al., 2018) 。给定模型\(f\)和样本\(x\)(正常或对抗样本),LID检测方法抽取深度神经网络每一个中间层的特征,然后使用公式 (7.1.4) 估计\(LID( x)\)。这里需要注意的是,\(LID( x)\)的估计需要知道\(x\)到其\(k\)-近邻的距离,所以\(x\)需要放在一批中数据里去估计。基于正常和对抗样本的LID特征可以训练最终的对抗样本检测器,具体的步骤参考算法 图7.2.4 。LID检测方法表现出了比KDE更优的检测结果,且可以在简单攻击(如FGSM)上训练后用以检测更复杂的攻击(如C&W攻击)。LID检测在MNIST、CIFAR-10和SVHN数据集上对五种攻击(包括FGSM、两种BIM变体、JSMA和C&W)的平均检测AUC为97.56%(MNIST)、91.90%(CIFAR-10)和95.51%(SVHN)。

图7.2.4 算法 训练LID对抗样本检测器¶
后来,Athalye等人在其工作中声称LID检测器并不能检测高置信度的对抗样本 (Athalye et al., 2018) ,但后续工作表明LID检测器并不存在此问题 (Lee et al., 2018) 。与KDE不同,LID的计算并不是可微的(涉及到\(k\)-近邻选择),所以通过简单的正则化(比如控制对抗样本的LID值变低)并不能得到更强的对抗攻击,无法攻破LID检测器。从这个角度来说,设计不可微且不易被近似 (Athalye et al., 2018) 的对抗样本检测方法似乎是构建更鲁棒的对抗样本检测器的一个可行思路,至少会在一定程度上增加攻击的难度。提的一提的是,近期有个LID的改进工作 (Lorenz et al., 2022) 将对多种攻击的检测AUC提高到了接近100%(近乎完美的检测),当然这个方法的实际效果和鲁棒性还有待进一步确认。
马氏距离。 马氏距离(Mahalanobis distance,MD)是度量学习中一种常用的距离指标,由Mahalanobis在1936年提出 (Mahalanobis, 1936) 。马氏距离衡量的是一个数据点\(x\)与一个分布\(Q\)之间的距离。假设分布\(Q\)的样本均值为\(\mu\),样本分布的协方差矩阵为\(\Sigma\),则样本\(x \in Q\)的马氏距离定义为:
相应的,两个样本\(x_i\)与\(x_2\)之间的马氏距离为:
马氏距离在协方差矩阵是单位向量时(各维度独立同分布)等于欧氏距离。实际上,马氏距离相当于欧式距离加一个白化转换(whitening transformation),把由多维随机变量组成的向量通过线性转换表示为一组不相关且方差为1的新变量。
Lee等人 (Lee et al., 2018) 提出使用马氏距离来检测对抗样本和分布外(out-of-distribution,OOD)样本。给定模型\(f\)和训练样本集合\(D\),样本\(x\)的马氏距离可以通过以下公式计算:
其中,\(f^{L-2}\)表示深度神经网络的倒数第二层输出(暂且称其为深度特征),\(\mu_c\)为类别\(c\)样本的深度特征均值,\(\Sigma_c\)为类别\(c\)样本间的协方差矩阵,类别\(c\)可以选为马氏距离最小的类。均值和协方差矩阵的定义如下:
其中,\(X_c\)表示类别为\(c\)的训练样本子集,\(N_c\)表示类别\(c\)样本的数量(即\(N_c=|X_c|\))。跟Ma等人的LID检测一样,Lee等人提出在神经网络的所有中间层上计算马氏距离,同时通过向样本\(x\)中添加可最小化马氏距离的噪声的方式进一步提高不同类型样本的区分度。详细的步骤参见算法 图7.2.5 ,其中加权置信度评的权重\(\alpha_l\)可以在一小部分认证数据集上训练逻辑回归模型得到。

图7.2.5 基于马氏距离的对抗样本检测¶
Lee等人 (Lee et al., 2018) 在CIFAR-10、CIFAR-100、SVHN数据集和ResNet、DenseNet模型上进行了对抗样本检测实验,发现其相比基于欧氏距离的KDE检测和LID检测有明显的性能提升,尤其是在面对一些弱攻击(如Deepfool)或者未知攻击的时候。基于ResNet模型的结果显示,马氏距离检测在三个数据集上的平均检测AUC分别达到了96.73%(CIFAR-10)、93.43%(CIFAR-100)、96.16%(SVHN)。虽然检测性能优秀,至于马氏距离为什么更适合做对抗样本检测仍需更多理解,此外,马氏距离能否提高其他检测方法也是一个值得探索的问题。
7.2.4. 预测不一致性¶
由于对抗样本是基于模型的梯度信息生成的,所以会导致对抗样本会过度依赖模型信息,在对样本进行随机变换或者向样本中添加随机噪声时,会产生很高的预测不一致性(比如发生类别翻转)。这意味着,在推理阶段当扰动噪声和模型参数之间的强关联被打破时,模型的预测结果会发生改变。基于此假设,可在推理过程中引入一定的随机性,并根据模型的预测结果变化来判定输入样本是否为对抗样本。从高维非线性假说的角度来理解,对抗样本位于高维空间的低概率区域,本质上具有高度推理不稳定性和预测不一致性。
贝叶斯不确定性。一个非常具有代表性的检测方法为贝叶斯不确定性(Bayesian uncertainty),由Feinman等人在其KDE的工作 (Feinman et al., 2017) 中提出。贝叶斯不确定性方法巧妙的使用了随机失活(dropout) (Srivastava et al., 2014) 技术,在推理阶段保持随机失活开启状态(通常情况下随机失活在推理阶段是关闭的),同时对样本进行多次推理并计算模型预测结果的方差(\(\mathrm{Var}(p) = \mathbb{E}(p^2) - [\mathbb{E}(p)]^2\))。具体的计算公式如下:
其中,\(\hat{ y}_i\)表示在第\(i\)次推理时得到的模型输出概率向量。贝叶斯不确定性在贝叶斯模型(如高斯过程)中有广泛的研究,使用随机失活训练得到的深度神经网络可以被看做是深度高斯过程(deep Gaussian process)的一种近似 (Gal and Ghahramani, 2016) 。在这里,随机失活开启状态的神经网络是一个随机化的模型,每一次前传都相当于从大网络中随机抽样一个小网络 (Hendrycks and Gimpel, 2016) 。
基于正常样本和对抗样本的贝叶斯不确定性特征可以训练一个逻辑回归模型(其他模型也可以,一般性能差别不大)进行对抗样本检测。在MNIST、CIFAR-10和SVHN数据集上的实验结果显示,推理不确定性可以检测一些经典的攻击方法如FGSM、JSMA和C&W攻击,但是无法检测BIM攻击。Feinman等人将其与KDE结合训练了一个组合特征检测器,发现贝叶斯不确定性与KDE有一定的互补性,在MNIST和SVHN数据集上整体的检测性能很好(AUC高于90%),但是在CIFAR-10数据集上效果欠佳(AUC为85.54%)
Carlini和Wagner的测试结果显示,贝叶斯不确定性在MNIST数据集上可以检测75%的C&W攻击,在CIFAR-10上可以检测95%的C&W攻击(相比MNIST效果更好了),即使对一般的适应性攻击(adaptive attack),也能检测出60%的对抗样本。最后,Carlini和Wagner基于目标模型随机采样了很多子网络,然后基于子网络集合进行攻击,最后能98%绕过推理不确定性检测 (Carlini and Wagner, 2017) ,代价是大大增加了攻击所需的扰动大小。在Carlini和Wagner所测试的10种检测方法中,推理不确定性检测方法是最鲁棒的,绕过检测需要对抗扰动的大小接近或超过人眼不可察觉的上限。
特征压缩。Xu等人 (Xu et al., 2018) 提出使用特征压缩(feature squeezing)方法对输入样本进行物理降维,然后根据模型在压缩前后的输出变化检测对抗样本。这里,“特征压缩”是指压缩输入空间而非深度特征空间。物理降维指的是直接减少输入图像的表示比特位数,使用更少的比特数来表示图像,以达到输入维度压缩的目的。此想法与线性假说不谋而合,降低输入维度可以提高模型对微小输入扰动的鲁棒性,于此同时降低比特数还可以降低像素精度,对噪声也起到一定的阻断作用。一般RGB图像的颜色深度(color depth)为8比特,即使用8个比特来表示像素值(0-255),其可以被压缩到更少的比特数,如7或1比特,而对于灰度图像(如MNIST)也可以通过二值滤波(binary filter)进一步压缩。给定原始比特位数8-bit,目标比特位数\(i\)-bit(\(1 \leq i \leq 7\)),原始像素值\(v\)可以通过下面的整数舍入操作进行压缩:
除了比特位压缩,Xu等人还探索了空间平滑(模糊)技术,包括局部平滑技术中值滤波(median filtering)和非局部平滑技术非局部平滑滤波(non-local means)。基于此,Xu等人使用模型输出变化的\(L_1\)范数(\(\|f( x) - f( x_s)\|_1\))来检测对抗样本。在MNIST、CIFAR-10和ImageNet上的实验结果显示,特征压缩方法可以直接提高模型的鲁棒性(模型对压缩后的对抗输入做出了正确预测),在三个数据集上都表现出了优异的效果。于此同时,特征压缩还可以跟对抗训练(当前最鲁棒的模型训练方法)结合,进一步提升鲁棒训练模型在更大对抗扰动下的鲁棒性。在检测方面,最优的特征压缩组合技术对FGSM、BIM、DeepFool、JSMA、C&W攻击的检测AUC达到了99.44%(MNIST)、94.74%(CIFAR-10)和94.24%(ImageNet)。
随机输入变换。此类方法通过对输入样本进行随机变换,然后根据模型预测的不一致性检测对抗样本。Tian等人 (Tian et al., 2018) 提出使用随机图像变换,并基于变换前后的逻辑(logits)输出来检测对抗样本。研究者基于9种随机平移和5种随机旋转组合成45种随机变换,然后基于模型的逻辑向量训练了基于简单全连接网络的对抗样本检测器。在MNIST和CIFAR-10上的结果显示,上述方法可以有效检测各种攻击强度的C&W攻击。此外,研究者通过类似二级分类法的策略,在适应性攻击下也能较为准确的检测C&W攻击,在FGSM和BIM攻击上检测效果更好。类似的方法正在被陆续的探索中,比如近期Wang等人 (Wang et al., 2022) 提出使用风格转换检测对抗样本。
Roth等人 (Roth et al., 2019) 向输入样本中添加随机噪声,然后基于模型的逻辑输出变化来计算对数几率(log-odds)指标并以此来检测对抗样本。给定输入样本\(x\),此检测方法向\(x\)添加随机噪声\(\eta \sim \mathcal{N}\)(\(\mathcal{N}\)为高斯噪声)得到噪声样本\(x+\eta\),通过比较模型在\(x\)上的逻辑向量\(z( x)\)与在\(x+\eta\)上的逻辑向量\(z( x+\eta)\)之间的差异来判别\(x\)是否为对抗样本。假设是对于正常样本\(z( x) \approx z( x+\eta)\),而对抗样本则会产生较大差异。通过设定恰当的阈值,该方法在CIFAR-10和ImageNet数据集上都展现了极高的检测准确率,比如在标准VGG、ResNet、WideResNet和Inception V3模型上检测PGD攻击的准确率高达99%以上,也能以较高的准确率检测未知攻击和适应性攻击。通过对数几率还可以进行预测结果修正,提高模型的对抗鲁棒性。Tramèr等人对此方法进行了攻击性评估 (Tramer et al., 2020) ,发现可以被特定的适应性攻击绕过,比如在对抗扰动\(x\)(类别为\(y\))的同时可以让\(z( x_{\textup{adv}})\)无限接近一个其他类别\(y'\neq y\)的干净样本\(x'\),即\(\min \|z(x_{\textup{adv}}) - z( x')\|\)。在此基础上加上EOT攻击技术可以完全绕过基于对数几率的检测器。
Hu等人 (Hu et al., 2019) 提出了一种跟对数几率类似的方法,但是使用了更聪明的噪声策略。直观来讲,如果一个样本被攻击过,那么再生成对抗攻击时会呈现出特殊属性:(1)梯度更均匀,即对抗样本的所有输入维度都具有类似的梯度大小;(2)二次攻击更难,已经被攻击过一次的样本较难进行第二次攻击(即对生成的对抗样本继续进行攻击)。基于此,Hu等人提出两个检测对抗样本的准则:(a)向输入样本x中添加随机噪声是否会导致模型的概率输出发生较大改变,如果“是”则为对抗样本(此方法与对数几率相同);(b)攻击输入样本x是否需要很多的扰动步数,如果“是”则为对抗样本。基于此组合方法,Hu等人展示了即便是白盒适应性攻击也难以躲避检测,因为这两个检测准则难以同时绕过。但是Tramèr等人的测试结果显示,可以同时绕过这两个检测准则的攻击是存在的 (Tramer et al., 2020) 。比如,给定正常样本\(x\),首先生成一个高置信度的对抗样本\(x_{\textup{adv}}\),然后在\(x\)和\(x_{\textup{adv}}\)之间基于二分查找,寻找对随机噪声具有高置信度同时离决策边界很近的对抗样本。 总体来说,对输入进行随机变换或者向输入添加随机噪声会引入随机性,提高对对抗样本的检测效果,但仍可能会被更有针对性的适应性攻击或者基于EOT的攻击绕过。
7.2.5. 重建不一致性¶
基于重建不一致性的检测方法假设:正常样本可以重建而对抗样本无法重建。原因是对抗样本已经跨过决策边界进入了另一个类别,重建时会按照另一个类别进行重建。此研究方向上最具有代表性的工作是Menghe和Chen提出的MagNet (Meng and Chen, 2017) 。
MagNet在正常样本上训练一个自编码器(autoencoder),然后通过重建结果构建一个检测器和一个改良器(reformer)。检测器通过重建错误或者模型在重建样本上的预测不一致性来检测对抗样本,而改良器将检测为“良性”的样本(包含正常样本和弱对抗样本)投影到离正常数据流形更近的位置,以达到进一步改良的目的。检测器所使用的重建错误定义为:
其中,\(x\)为要检测的测试样本,\(AE( x)\)为自编码器重建的样本,\(\|\cdot\|_p\)为\(L_p\)范数,其中\(p=1,2\)。
检测器还可以基于JS散度(Jensen-Shannon divergence)的预测不一致性\(JSD(f( x)/\tau,f(AE( x))/\tau)\)进行检测,其中\(\tau\)为温度参数(\(\tau=10,40\))。对抗样本检测可以基于预先定义的阈值进行。改良器可以使用已训练好的自编码器,使用重建样本\(AE( x)\)代替原始样本以达到改良的目的。此外,Menghe和Chen提出充分利用集成防御和随机变换的优势,训练多个自编码器、检测器和改良器来构造更鲁棒的灰盒检测防御机制。
但是,Carlini和Wagner在后续的评估中发现,MagNet检测可以被类似EOT的方法绕过 (Carlini and Wagner, 2017) 。 Carlini和Wagner构造了更多的自编码器,并基于此生成迁移性更强C&W攻击,发现MagNet无法检测此类灰盒攻击。 Jin等人提出一个类似MagNet的重建方法APE-GAN(adversarial perturbation elimination GAN),利用对抗生成网络(GAN)来复原(并非检测)对抗样本,以此来提高模型的推理鲁棒性 (Jin et al., 2019) 。与普通GAN不同,APE-GAN的生成器\(G(\cdot)\)是一个自编码器,输入对抗样本输出复原的样本,并在FGSM对抗样本上进行训练。Carlini和Wagner的评估测试 (Carlini and Wagner, 2017) 发现,这种基于重建的模型防御方法可以轻易的被白盒适应性C&W攻击破坏掉,攻击生成的样本会造成更大的重构错误,超出了重建器\(G(\cdot)\)的处理能力。这些研究结果说明基于重建不一致性的检测面临一个很现实的挑战,那就是对抗攻击可以生成既能攻击又能重建的对抗样本。
7.2.6. 诱捕检测法¶
现有大部分对抗样本检测方法并不会修改模型。实际上,我们是可以修改模型的,通过一种特殊的训练方法让模型符合一定的特性,从而诱导对抗样本违反这种特性,而被检测出来。我们将此类方法称为诱捕检测方法。代表方法为Pang等人提出的逆交叉熵(reverse cross entropy)训练 (Pang et al., 2018) 和Dathathri等人提出的神经指纹(neural fingerprinting,NeuralFP) (Dathathri et al., 2018) 。两种方法都是将模型的概率输出训练到符合一种特定的分布,从而让不符合分布的对抗样本更容易暴露出来。
对抗样本的对抗性往往使得模型以较高置信度预测对抗目标类别,所以相比正常样本来说概率向量的熵会更低。那么,如果在训练模型时增高其输出概率分布的熵,则会让对抗样本更容易被识别出来。Pang等人的逆交叉熵损失函数就是基于此思想提出的,具体定义如下:
其中,\(f( x)\)为模型的概率输出,\(R_y\)是逆类别向量,其在\(y\)所对应位置上的概率是0,其他位置(\(i\neq y\))上的概率为\(\frac{1}{C-1}\)(\(C\)为总类别数)。使用逆交叉熵损失训练的模型会让模型在非\(y\)位置上的概率分布趋向于均匀(高熵)。在检测阶段,使用核密度估计 (Feinman et al., 2017) 作为检测指标,衡量预测结果的非最大熵( non-maximal entropy),即除去预测类别位置以外的概率向量的熵。核密度估计的使用如下:
其中,\(X_{\hat{y}}\)表示类别和预测类别\(\hat{y}\)相同的训练样本子集,\(z_i\)和\(z\)是模型的逻辑输出,\(k( z_i, z)=\exp(-\| z_i - z\|^2/\sigma^2)\)是带宽为\(\sigma\)的高斯核。基于\(KDE( x)\)分布,可以设置合理的阈值进行对抗样本检测,当然也可以单独训练一个检测器。
在MNIST和CIFAR-10上的结果表明,使用逆交叉熵训练的模型性能与标准交叉熵函数训练的模型性能一致,但是可以明显提高对抗样本的检测AUC,并且可以在一定程度上防御白盒适应性攻击。
Dathathri等人 (Dathathri et al., 2018) 提出神经指纹(NeuralFP)方法,在模型训练阶段显式的学习特定的“输入变化-输出变化”对应关系\((\Delta x, \Delta y)\),从而在测试阶段可以通过检测输入输出变化来检测对抗样本。首先,对于一个\(C\)类分类问题,定义包含\(N\)个指纹样本的指纹数据如下:
其中,\(\mathcal{X}^{i,j}\)是类别\(j\)的第\(i\)个指纹,这些指纹(即对应关系)可以由防御者指定。值得注意的是,输入变化\(\Delta x^i\)是独立于类别(class-dependent)的,而输出变化是依赖于类别(class-independent)的。下面的比较函数(comparison function)定义了模型在指纹数据上的“错误”:
在训练过程中,最小化上述指纹错误可以将指纹嵌入到模型内部。在测试阶段,我们可以检测测试样本\(x\)的指纹错误,在大于某个阈值时会被检测为对抗样本。
可以看出,神经指纹方法通过让模型符合一定的性质来诱导对抗攻击去打破这种性质,显现出明显的预测不一致性。实际上,指纹数据的特殊对应关系会强制模型在决策边界附近进行空间重整形(spatial reshaping),形成某种特定形状的边界空间。借助巧妙的设计,此方法可以将对抗样本排除在边界空间之外,使其无法在限定的扰动大小范围内通过此空间跨过决策边界。在MNIST和CIFAR-10上的实验结果显示,神经指纹方法在检测FGSM、JSMA、BIM和C&W等常见攻击时可以达到98%以上的AUC,且在大部分情况下达到近乎100%的AUC。这充分体现了诱捕类检测方法的强大,只要利用合理,完全可以诱导对抗样本暴露其对抗本性。未来研究可进一步探索如何对决策边界空间或者模型内部空间进行更为广泛的指纹覆盖。
7.3. 对抗训练¶
对抗训练是已知最有效的对抗防御方法,其通过在对抗样本上训练模型来提升模型自身的鲁棒性。此外,对抗训练以及前面介绍的对抗样本检测是领域内研究最多的两种防御方式,其中对抗训练可以认为是一种主动防御而对抗样本检测则是一种被动防御。“主动”是指模型本身是鲁棒的,而“被动”是指模型本身不鲁棒但是可以对潜在攻击进行检测并拒绝服务。对抗训练的概念在对抗样本发现的早期就已经被提出了,只是在2018年才取得重要突破。2018年以后,大量对抗防御工作大都基于对抗训练进行,或者提出更优的对抗训练方法,或者将对抗训练与其他防御策略结合来提高防御效果。
对抗训练具有以下特点:
鲁棒性最佳:对抗训练是目前已知最鲁棒的对方防御方法。
方法简单:对抗训练可直接训练一个对抗鲁棒的模型,不依赖(但是可以叠加)额外的输入去噪、对抗检测等辅助防御策略。
训练耗时:对抗训练耗时大约是正常训练的8-10倍。 比如,在CIFAR-10数据集上使用过4块2080Ti GPU对抗训练WideResNet34-10模型大约需要40小时;在ImageNet数据集对抗训练ResNet-50模型大约需要128块V100 GPU 52小时 (Xie et al., 2019) 。
容易过拟合:对抗训练更容易过拟合到训练数据,加大训练和测试性能之间的差距。例如,PGD对抗训练在CIFAR-10数据集上可以达到90%以上的训练鲁棒性,而对抗鲁棒性却只有45%-50%。
降低性能:经过对抗训练的模型在自然(干净)测试样本上通常会有不同程度的性能下降。例如,在CIFAR-10数据集上,若以\(L_{\infty}=8/255\)的扰动大小进行对抗训练,大约会导致10%的自然准确率下降;在ImageNet数据集上,则会有8%-15%的下降 (Xie et al., 2020, Xie et al., 2019) 。
7.3.1. 早期对抗训练方法¶
对抗训练的思想比较直观,由于深度神经网络具有强大的学习能力,那么让网络直接学习对抗样本就可以获得对抗鲁棒性。所以对抗训练在对抗样本(而不是普通样本)上训练模型。当然,很多早期的对抗训练方法大都采用混合训练的方式,即同时在对抗样本和正常样本上训练模型。下面三个工作可以认为是对抗训练领域三个里程碑式的工作:
2014年,Goodfellow等人首次提出对抗训练的概念,为鲁棒优化和正则化研究开启了新大门 (Goodfellow et al., 2015) 。
2018年,Madry等人提出基于PGD的对抗训练方法给对抗训练的性能带来巨大提升,使对抗训练成为主流对抗防御方法 (Madry et al., 2018) 。
2019年,Zhang等人提出基于KL散度的对抗训练方法TRADES,大幅提升了Madry等人提出的PGD对抗训练,极大的推动了对抗训练的研究热潮 (Zhang et al., 2019) 。
虽然对抗训练直到2018年才取得重要进展,但从2013年发现对抗样本到2018年期间,很多对抗训练方法已经被提出,而且有些方法提出的优化框架与2018年以后的框架几乎是一样的。可以说,这些早期的对抗训练方法奠定了对抗训练的研究基础。
早在2013年,Szegedy等人 (Szegedy et al., 2014) 在揭示对抗样本现象的同时就已经探索了对抗训练。他们采用了一种交替“生成-训练”的方式,在训练过程中对神经网络的每一层(既包含输入层也包含中间层)生成对抗样本,然后将这些对抗样本加入原始训练集进行模型训练,发现深层对抗样本对鲁棒泛化更有用。Szegedy等人将对抗训练解释为是一种正则化方法,并对其他正则化方法,如权重衰减(weight decay)和随机失活(dropout)等,也进行了分析。可惜由于Szegedy等人使用的对抗样本生成算法L-BFGS的优化代价比较高,最终训练框架的实用性并不是很好 (Goodfellow et al., 2015) 。
FGSM对抗训练。 Goodfellow等人在其线性假说工作 (Goodfellow et al., 2015) 中提出基于快速对抗攻击方法FGSM的对抗训练方法,同时在普通和FGSM对抗样本上训练模型。具体的优化目标如下:
其中,\(\mathcal{L}_{\textup{CE}}\)是交叉熵损失函数,\(x_{\textup{adv}}\)是\(x\)的对抗样本,通过第二行的单步FGSM攻击生成;\(\alpha\)是调和两部分损失的权重系数(实验中设为0.5)。值得注意的是,Goodfellow等人并未使用中间层的对抗样本,因为他们发现中间层对抗样本并没有用。
实际上,上式可以化简成min-max优化的标准形式:
其中,内部最大化是生成对抗样本\(x_{\textup{adv}}\)的过程,优化变量是\(x_{\textup{adv}}\);而外部最小化是在普通样本\(x\)和对抗样本\(x_{\textup{adv}}\)上训练模型的过程,优化变量是模型参数\(\theta\)。FGSM对抗训练的优点是训练速度快,相比传统的模型训练只需要增加一次前传和后传,缺点是无法防御多步对抗攻击,如BIM、PGD攻击等 (Kurakin et al., 2016, Wong et al., 2020) 。
公式 (7.3.2) 已经跟Madry等人提出的PGD对抗训练的优化目标很接近了,删掉\(\alpha\mathcal{L}_{\textup{CE}}\)项得到的便是PGD对抗训练的优化目标(剩余项的系数可以忽略)。而这正是Nokland在其工作 (Nøkland, 2015) 中所做的,完全在对抗样本上训练模型,并基于此“对抗反向传播”(adversarial back-propagation)正则化方法提升模型的泛化能力(并未对对抗鲁棒性进行测试)。所以Nøkland对抗训练的优化目标跟Madry等人的PGD对抗训练是完全一致的,虽然Nøkland并未在其论文中给出具体定义(后面会介绍第一次显式定义实际上是由Huang等人 (Huang et al., 2016) 、Shaham等人 (Shaham et al., 2015) 以及Lyu等人 (Lyu et al., 2015) 在同一时期给出的)。 具体来说,FGSM对抗训练和Nøkland对抗训练都使用FGSM算法来求解内部最大化问题,而Madry等人提出的PGD对抗训练使用PGD算法来求解内部最大化问题。当然这两类方法之间还存在其他一些“小区别”,我们将在后续小节介绍,也正是这些看似简单的“小区别”让PGD对抗训练远远好于FGSM对抗训练。
Goodfellow等人还提出了对对抗训练的六种理解:
对抗训练是一种基于数据增广的训练方式,而对抗样本生成就是一种特殊的数据增广;
对抗训练是一种正则化技术;
对抗训练相当于优化模型在最差情况(worst-case)下的错误;
对抗训练相当于最小化模型在噪声输入上的期望错误上界;
对抗训练是一个对抗博弈(adversarial game)的过程;
对抗训练是一种主动学习(active Learning),模型在训练过程中主动请求标注新的样本(即对抗样本)。
这些不同层面的理解也引发了后续工作从不同的方向对对抗训练进行探索与改进。
下面介绍三个几乎是在同一时间(论文上传至arXiv的时间都在2015年7月-11月之间)公布的代表性工作。
虚拟对抗训练。 Miyato等人 (Miyato et al., 2016) 从提高模型泛化和正则化的角度对对抗训练进行了探索,提出了基于KL散度的虚拟对抗训练(virtual adversarial training,VAT)方法。在训练过程中,VAT通过在训练样本周围生成“虚拟”对抗扰动的方式来提高模型的局部分布平滑度(local distribution smoothness)。这里,“虚拟”对抗扰动实际上就是对抗扰动,局部分布平滑指的是样本\(x\)周围的平滑。VAT的优化目标定义如下:
其中,\(\mathcal{L}_{\textup{CE}}\)为交叉熵损失函数,\(\mathcal{L}_{\textup{KL}}\)为KL散度损失函数;\(x\)是原始训练样本,\(x_{\textup{adv}}\)是基于\(x\)生成的对抗样本,\(\epsilon\)是\(L_2\)范数定义的扰动上限。为了着重突出VAT的思想,上式对原始的VAT方法进行了一定的符号化简。在VAT中,\(-\mathcal{L}_{\textup{KL}}(f( x), f( x_{\textup{adv}}))\)项被定义为局部分布平滑(local distributional smoothing,LDS)。值得注意的是,VAT是从提高模型泛化的角度提出的,所以在原论文中并未对其进行对抗鲁棒性测试。VAT在解内部最大化问题时使用了单步的幂迭代法(power iteration)方法 (Golub and Van der Vorst, 2000) ,其等同于FGSM算法。所以VAT跟基于\(L_2\)范数的FGSM对抗训练十分接近,区别是FGSM对抗训练使用的是\(\mathcal{L}_{\textup{CE}}\)损失而VAT使用的是\(\mathcal{L}_{\textup{KL}}\)损失。实验表明,在提高模型泛化方面,VAT只比FGSM对抗训练好一点点。实际上,VAT的优化目标跟后来Zhang等人提出的基于KL散度的TRADES (Zhang et al., 2019) 对抗训练是一样的。
Min-max鲁棒优化。 如前面提到的,2015年-2016年左右的很多对抗训练工作实际上都是在解 min-max优化问题,但第一次显式将对抗训练定义为min-max优化问题是由Huang等人 (Huang et al., 2016) 、Shaham等人 (Shaham et al., 2015) 以及Lyu等人 (Lyu et al., 2015) 在大约同一时间完成的。在这里我们采用Huang等人的定义进行介绍。结合Goodfellow等人提出的FGSM对抗训练 (Goodfellow et al., 2015) 、Nøkland提出的对抗反向传播 (Nøkland, 2015) 、Miyato等人提出的虚拟对抗训练 (Miyato et al., 2016) ,Huang等人提出统一的min-max优化框架:
其中,\(\mathcal{L}\)可以是任意分类损失函数,\(r\)为对抗扰动,\(\|\cdot\|\)可以是任意范数(\(L_{1,2,\infty}\)),\(sign(\cdot)\)是符号函数。当损失函数\(\mathcal{L}\)为交叉熵损失函数时,不同扰动范数下的对抗噪声可以通过下面的方式生成:
如果\(\|\cdot\|\)是\(L_2\)范数,那么\(r^*=\epsilon\cdot\frac{\nabla _{ x}\mathcal{L}(f( x),y)}{\|\nabla _{ x\mathcal{L}(f( x),y)}\|_2}\);
如果\(\|\cdot\|\)是\(L_{\infty}\)范数,那么\(r^* = \epsilon\cdot sign(\nabla _{ x}\mathcal{L}(f( x),y))\);
如果\(\|\cdot\|\)是\(L_1\)范数,那么\(r^* = \epsilon\cdot \mathbf{m}_k\),其中\(\mathbf{m}_k\)为位置\(k\)处值为1其他位置值为0的掩码矩阵,\(k\)是\(|\nabla _{ x}\mathcal{L}(f( x),j)|_k=\|\nabla _{ x\mathcal{L}(f( x),y)}\|_{\infty}\)的位置。
Huang等人将上述基于\(L_2\)范数的对抗训练命名为对抗学习(learning with adversarial,LWA)方法,并实验展示了其相对FGSM对抗训练的优越性。Huang等人同时提出了基于神经网络中间层特征的对抗训练方法,但效果并没有输入空间的对抗训练好。
上述早期对抗训练方法(主要是FGSM对抗训练)的特点可以总结为以下两点:
训练速度较快,虽然比普通训练更耗时但是比后面多步的对抗训练方法要高效很多;
易过拟合到弱对抗样本,所训练的模型对较弱的FGSM攻击很鲁棒,但是对更强的PGD攻击鲁棒性就很差。
下面将介绍2018年以后的对抗训练方法。
7.3.2. PGD对抗训练¶
2018年,Madry等人 (Madry et al., 2018) 提出从鲁棒优化的角度去解决深度神经网络的对抗鲁棒性问题。具体来说,Madry等人将考虑了对抗因素的模型训练看做一个鞍点(saddle point)问题,定义如下:
上式对原论文中的定义进行了等价化简,得到形式上与Huang等人的min-max优化框架(公式 (7.3.4) )一致的定义。实际上,上式定义的min-max优化问题在鲁棒优化领域有着悠久的历史,最早可以追溯到Wald的工作 (Wald, 1939, Wald, 1945, Wald, 1992) 。 上述鞍点问题由内外两层优化组成,即内部最大化(inner maximization)问题和外部最小化(outer minimization)问题。内部最大化问题的目标是生成更强的对抗样本,而外部最小化问题的目标是最小化模型在(内部最大化过程中生成的)对抗样本上的损失,求解上述鞍点问题的过程也就是对抗训练的过程。
Madry等人从鲁棒优化的角度研究了式 (7.3.5) 的鞍点问题,并提出使用PGD(projected gradient descent)算法求解内部最大化问题,定义如下:
其中,\(\text{Proj}_{ x+\mathcal{S}}\)是一个投影操作,将对抗样本约束在以\(x\)为中心的高维球\(x+\mathcal{S}\)之内;\(x^{t}\)和\(x^{t+1}\)分别是第\(t\)步(总步数为\(T\))对抗攻击产生的对抗样本;\(\alpha\)是单步步长,其大小要求能探索到\(\epsilon\)-球以外的空间(即\(\alpha T > \epsilon\))。
PGD对抗训练也经常被称为标准对抗训练(standard adversarial training)或者Madry对抗训练(Madry adversarial training)。PGD算法实际上是求解有约束min-max问题的一阶最优算法,所以PGD攻击也可以被认为是最强的一阶攻击算法。关于PGD攻击算法,读者可以在章节 6.1节 找到详细的介绍。同时,Madry等人还研究了对抗性鲁棒性和模型大小之间的关系,发现对抗鲁棒的模型往往需要更多的参数。此外,他们证明了对抗训练可以获得一个具有对抗鲁棒性的模型。
PGD攻击与BIM攻击高度相似,只存在两个“小区别”:(1)步长设置,PGD并没有限制步长大小(BIM的步长为\(\epsilon/T\),PGD往往采用更大的步长);(2)随机噪声初始化,PGD在攻击开始前有一个随机噪声初始化的操作\(x_{\text{adv}}^{0} = x + \mathcal{U}(- \epsilon, + \epsilon)\),其中\(\mathcal{U}(- \epsilon, + \epsilon)\)为\([- \epsilon, + \epsilon]\)之间的均匀分布。实验表明,这两个“小区别”是PGD对抗训练显著优于FGSM或是BIM对抗训练的关键。在差不多同一时间,Tramèr等人 (Tramèr et al., 2018) 也发现在FGSM对抗训练的基础上加随机噪声初始化会大幅提高模型鲁棒性。
2017年,Kurakin等人 (Kurakin et al., 2016) 发现单步对抗训练不能防御多步攻击,即使是使用多步BIM方法训练也是如此。 2019年,Wong等人 (Wong et al., 2020) 在探索快速单步对抗训练方法的时候,发现添加了上述两个操作的FGSM对抗训练能达到与PGD对抗训练相当的鲁棒性。直观理解,随机噪声初始化可以有效防止攻击算法因样本\(x\)周围高低不平的损失景观(loss landscape)而卡在局部最优的位置;而使用较大步长配合投影操作有助于在\(\epsilon\)边界附近增加探索,找到更强的对抗样本。
式 (7.3.5) 中定义的min-max优化问题经常与对抗生成网络(GAN)的min-max优化问题混淆。二者的区别包括(但不仅限于)以下几点:
PGD对抗训练是有约束(即\(\epsilon\)约束)的min-max优化问题(constrained min-max optimization problem),而GAN的训练是一个无约束的min-max优化问题;
PGD对抗训练只涉及一个模型(是一个自我对抗的过程),而GAN涉及两个模型(是一个相互对抗的过程);
PGD对抗训练得到一个判别模型(学习的是类别间的决策边界),而GAN得到的是生成模型(学习的是单类别的分布)。
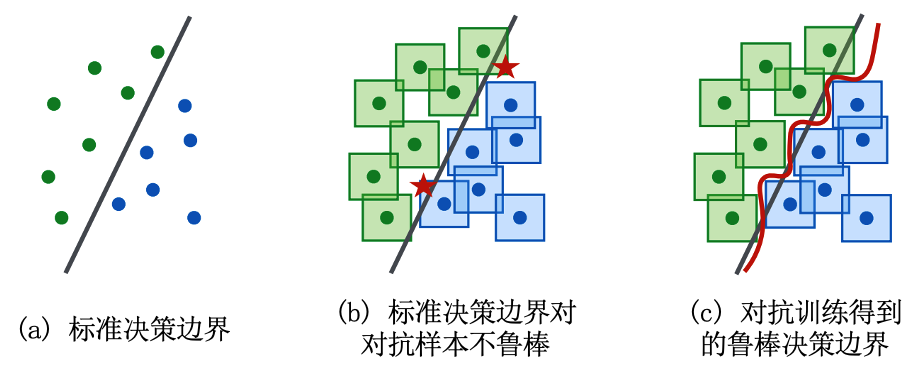
图7.3.1 对抗训练会得到鲁棒决策边界 (Madry et al., 2018)¶
PGD对抗训练所带来的显著鲁棒性提升让研究者们看到了训练对抗鲁棒模型的可能,后续出现了很多专门理解其工作原理的工作,以便进一步提升其鲁棒性。总结来说,PGD对抗训练及其变体具有以下特点:
鲁棒决策边界: PGD对抗训练可以让模型的决策边界更加鲁棒,即在输入样本周围一定范围内移动样本并不会跨过决策边界,如图 图7.3.1 所示;
通用鲁棒性:PGD对抗训练的模型可以同时防御单步、多步以及不同范数的对抗攻击;
需要大容量模型:PGD对抗训练需要更大尤其是更宽的深度神经网络模型;
需要更多数据:PGD对抗训练对数据量需求更高,增加训练数据可以获得明显的鲁棒性提升;
激活截断: PGD对抗训练的模型内部会产生类似激活截断的效果,可有效抑制对抗噪声对部分神经元的激活,进而阻断其在层与层之间的传递;
鲁棒特征学习: PGD对抗训练可以让模型学习到更鲁棒、解释性更好的特征,而普通训练则会学习到对泛化更有用但不鲁棒也不好解释的特征;
准确率-鲁棒性权衡: 模型的准确率(在干净样本上的准确率)和鲁棒性(在对抗样本上的准确率)之间存在冲突,二者(或许)不可兼得,在同一设置下,鲁棒性提升会降低准确率,反之亦然。
此外,我们在本章节开始介绍的对抗训练的五个特点,如鲁棒性最佳、训练很耗时、降低性能(即准确率-鲁棒性权衡)、容易过拟合等,也适用于PGD对抗训练。目前,准确率-鲁棒性权衡问题是制约对抗训练进一步发展的主要瓶颈。
对PGD对抗训练的改进方法有很多,可以通过设计更灵活的扰动步数、扰动步长、更好的协调内部最大化与外部最小化等方式进行提高。基于PGD对抗训练的集成学习和课程表学习是两种比较直观的改进方式。例如,Cai等人 (Cai et al., 2018) 提出基于攻击步数的课程表对抗训练,同时为了防止遗忘提出多步混合的累积学习方式。Tramèr等人 (Tramèr et al., 2018) 提出结合多个模型的集成对抗训练方法,由于训练中的对抗样本是集合了多个模型生成的,所以得到的模型一般对迁移攻击很鲁棒。而Yang等人 (Yang et al., 2020) 提出的DVERGE方法则通过在集成模型之间更好的分散对抗脆弱性来防御迁移攻击。当与PGD对抗训练结合时DVERGE集成策略展现了稳定的鲁棒性提升。
Ding等人 (Ding et al., 2019) 从边界最大化的角度分析了对抗训练,提出最大边界对抗(max-margin adversarial,MMA)训练方法,通过探索能最大化样本到决策边界的距离的扰动(这意味着每个样本都应该设置不同的扰动上界)来更好的权衡准确率和鲁棒性。Wang等人 (Wang et al., 2019) 分析了PGD对抗训练的内部最大化和外部最小化之间的相互作用,发现内部最大化对最终的鲁棒性影响更大,但其在训练初期并不需要生成很强的对抗样本。基于此,Wang等人提出一个一阶平稳条件(first-order stationary condition,FOSC)来衡量内部最大化问题解的收敛性,并在训练的不同阶段通过控制对抗样本的收敛性不断变好(FOSC值不断变小)来进行动态对抗训练(dynamic adversaRial training,DART)。
PGD对抗训练使用单一PGD攻击来解决内部最大化问题,可能会存在输入空间探索不足的问题。为了解决此问题,Dong等人 (Dong et al., 2020) 提出基于分布的对抗训练方法对抗分布训练(adversarial distributional training,ADT)。ADT通过向对抗噪声中添加高斯噪声并最大化输出概率的熵来生成覆盖性更好的对抗样本。为了解决PGD对抗训练的收敛性问题,Zhang等人 (Zhang et al., 2020) 提出友好对抗训练(friendly adversarial training,FAT)方法,通过一系列早停策略(如达到一定对抗损失即停止攻击)来生成更有利于模型训练的对抗样本,以此来稳定对抗训练。Bai等人 (Bai et al., 2020) 提出通道激活抑制(Channel-wise Activation Suppressing,CAS)对抗训练方法 ,将PGD对抗训练应用在深度神经网络的中间层来抑制对抗噪声对中间层的激活,进而提高中间层特征的对抗鲁棒性。此方法需要在要增强的中间层处外接一个辅助分类器来完成。
7.3.3. TRADES对抗训练¶
Zhang等人 (Zhang et al., 2019) 提出的TRADES(TRadeoff-inspired Adversarial DEfense via Surrogate-loss minimization)对抗训练方法是对PGD对抗训练的一个重要改进,此方法赢得了NeurIPS 2018对抗视觉挑战赛的对抗防御赛道第一名。其方法本身很简单,即使用KL散度代替交叉熵来作为对抗训练的损失函数。TRADES的优化目标如下:
其中,\(\mathcal{L}_{\text{CE}}\)是交叉熵损失函数,\(\mathcal{L}_{\text{KL}}\)是KL损失函数。上式中第一部分在干净样本\(x\)上最小化交叉熵分类损失是为了提高模型的分类准确率,而第二部分生成对抗样本并在对抗样本\(x_{\text{adv}}= x+ r\)上最小化KL散度可以被理解为是一种鲁棒性正则 (Zhang et al., 2019) 。
Zhang等人提出鲁棒分类错误(robust classification error)可以被分解为自然分类错误(natural classification error)和边界错误(boundary error),具体定义如下:
其中,TRADES对抗训练优化目标中的第一项和第二项分别对应自然错误和边界错误。基于上述分解,可以对对抗训练的准确率-鲁棒性权衡问题进行理论分析和更好的解决。此外,TRADES的内部最大化损失\(\mathcal{L}_{\text{KL}}(f( x), f( x+ r))\)是可以继续化简为交叉熵损失函数的,这是因为KL损失分解后的其中一项是常数项。再进一步,真实标签\(y\)和模型的预测分布\(f( x)\)之间是有关联的,基于此可以对TRADES继续化简成类似PGD对抗训练的形式,感兴趣的读者可以尝试一下。
在这里,我们介绍一些对TRADES的理解。基于KL散度的对抗损失会在训练的初期生成对模型“更有针对性”的对抗样本,因为其最大化对抗样本与干净样本之间的预测概率分布,对模型已经学到的预测分布产生反向作用,从而会阻碍模型的收敛。 所以TRADES对抗训练保留了在干净样本上定义的交叉熵损失函数,以此来加速收敛。相对来说,基于交叉熵损失函数的对抗训练的收敛性问题会轻一点,因为对抗损失是基于真实类别\(y\)定义的,所以在模型预测错误的样本上不会产生特别大的反向作用。比如,模型对样本\(x\)的预测是错误的,那么攻击后得到的对抗样本\(x_{\text{adv}}\)的预测也是错的,差别不大,模型继续向着正确的类别学习就好了。需要指出的是,虽然添加自然损失项\(\mathcal{L}_{\text{CE}}(f( x), y)\)可以提高收敛速度,但还是存在两个潜在的问题:(1)收敛不稳定,导致训练过程对超参\(\lambda\)比较敏感;(2)在大规模数据集如ImageNet上不稳定性会加剧,导致超参难调或鲁棒性能下降。
下面我们介绍两种“逻辑匹配”(logits pairing)的正则化方法,可以帮助从正则化的角度理解TRADES。这两种逻辑匹配方法分别是干净逻辑匹配(clean logits pairing,CLP)和对抗逻辑匹配 (adversarial logits pairing,ALP),均由Kannan等人 (Kannan et al., 2018) 提出。干净逻辑匹配解决下列优化问题:
其中,\(z(\cdot)\)表示模型的逻辑输出,\(x'\)是干净样本的配对样本(与\(x\)组成一对),可以通过给样本\(x\)添加随机噪声的方式来获得。CLP通过约束模型在样本对(\(x\),\(x'\))之间学习相似的逻辑分布来正则化模型的鲁棒性。有趣的是,如果我们将配对样本换成对抗样本,则CLP会变的与TRADES很相似:
唯一的区别是内部最大化选择的是\(L_2\)损失。
相应的,对抗逻辑匹配(ALP)的优化目标如下:
其中,第二项\(L_2\)损失只参与外部最小化,其正则化模型在自然和对抗样本之间学习相同的逻辑值,从而在对抗训练(第一项)的基础上对鲁棒性进行进一步提升。ALP与TRADES的相似点是,二者都在自然和对抗样本上训练模型,且形式上相似(都是一个最大化项加一个最小化项),区别是ALP基于交叉熵损失函数生成对抗样本,正则的是模型在两种样本上的逻辑值(而非决策边界)。 值得注意的是,ALP和CLP的对抗鲁棒性有待认证,因为Engstrom等人在后续工作 (Engstrom et al., 2018) 中指出ALP带来的对抗鲁棒性可能并不可靠。
7.3.4. 样本区分对抗训练¶
Wang等人 (Wang et al., 2019) 提出错误区分对抗训练(misclassification aware adversarial training,MART)方法,在对抗训练过程中对未正确分类的样本进行区别对待,增加对这些样本的学习力度和收敛性。此想法受启发于错误分类样本对最终的鲁棒性影响较大的观察。通过把样本分为正确分类和错误分类两类,MART将鲁棒风险分解为:
其中,\(\mathcal{R}_{\text{rob}}^{+}(f)\)为模型已正确学习的样本对应的风险,\(\mathcal{R}_{\text{rob}}^{+}(f)\)为模型尚未正确学习的样本对应的风险。需要注意的是,正确学习与否是针对干净样本来说的,而非对抗样本。基于此,MART提出优化下列min-max优化问题来训练鲁棒的模型:
其中,\(\mathcal{L}_{\text{BCE}}=-\log( p_y( x_{\text{adv}})) - \log((1-\max_{k\neq y} p_{k}( x_{\text{adv}})))\)为增强交叉熵损失(boosted cross entropy,BCE),\(p_{k}( x)\)表示模型对应类别\(k\)的概率输出。BCE损失通过拉高正确类别的概率同时压低最大错误类别的概率来增强学习,从而有利于模型在尚未正确学习的样本上的收敛。但其对抗样本的生成方式依然采用了标准的PGD攻击,因为大量研究证明用PGD求解内部最大化问题已经可以带来最优的鲁棒性。也就是说MART实际上只提高了外部最小化的部分,同时为了促进收敛将内部最大化方法由KL损失换回了交叉熵损失。MART针对TRADES的收敛性问题改进了其外部最小化的部分,且改进的核心在于如何区别对待错误分类的训练样本。
Zhang等人 (Zhang et al., 2020) 也对分对和分错的样本进行了区分对待,不过采用的方式与MART不同。其提出几何区分(geometric aware)的概念,通过样本被成功攻击的步数来计算样本离决策边界的距离,并根据这个距离给每个样本设置一个权重,进行加权对抗训练。其提出的几何区分样本重加权对抗训练方法(geometry-aware instance-reweighted adversarial training,GAIRAT)解决下面定义的min-max优化问题:
其中,权重计算函数\(\omega( x,y)\)定义如下:
其中,\(T\)表示使用PGD生成对抗样本时的总步数,\(\kappa( x,y)\)代表模型恰好误分类对抗样本时的步数。且对模型已经误分类的干净样本设置为一个固定的上限值比如1,当\(\omega( x,y)\equiv 1\)时,GAIRAT退化为PGD对抗训练。
7.3.5. 数据增广对抗训练¶
Alayrac等人 (Alayrac et al., 2019) 和Carmon等人 (Carmon et al., 2019) 同时在NeurIPS 2019会议上提出两个类似的对抗训练提升策略,即利用额外的训练数据来提升对抗鲁棒性。举例来说,使用从80 Million Tiny Images数据集(此数据集由于包含不合规图片已永久下线)中精心选择的100K或500K额外数据来提高模型在CIFAR-10数据集上的鲁棒性。在原始数据集\(D\)的基础上,两个工作通过相似的数据选择策略选择了未标注的额外数据\(D_{\text{ul}}\),然后在原始数据集和额外数据集上同时进行对抗训练:
其中,\(\hat{y}\)是未标注样本\(x_{ul}\)的预测类别\(f( x_{ul})\)。
有个隐藏的额外数据使用技巧是,外部数据必须要和原始数据集中的样本进行1:1混合训练才能够提升鲁棒性,否则(比如随机混合)不但不会提升反而还会降低鲁棒性。这说明外部数据更多的是起到了一种正则化的作用,通过增加更多样的训练数据来学习更加平滑的决策边界,但是这种正则化无法脱离原始训练数据。虽然并不是所有的数据集都可以找到一个合适的外部数据来协助提升鲁棒性,但是此类方法至少增加了我们对对抗鲁棒性的理解,即使用额外数据确实可以提高对抗鲁棒性。
Rebuffi等人 (Rebuffi et al., 2021) 研究了三种数据增广方式,即Cutout (DeVries and Taylor, 2017) 、CutMix (Yun et al., 2019) 和MixUp (Zhang et al., 2018) ,并结合TRADES对抗训练,发现结合了模型参数平均(model weight averaging,MWA) (Izmailov et al., 2018) 的CutMix可以显著提高对抗训练的鲁棒性。研究者将数据增广所带来的收益归因于多样化的数据对鲁棒过拟合(robust overfitting)问题 (Rice et al., 2020) 的缓解。实际上,此前已有工作将数据增广、逻辑平滑、参数平均等技巧用以解决鲁棒过拟合问题 (Chen et al., 2021, Rice et al., 2020) 。基于此,Rebuffi等人 (Gowal et al., 2021, Rebuffi et al., 2021) 提出进一步结合生成模型DDPM(denoising diffusion probabilistic model)与CutMix数据增广,在不借助任何外部数据的情况下取得了当前最优的对抗鲁棒性。此外,基于多种数据增广技术的自监督鲁棒预训练 (Shafahi et al., 2019) 也可以看做是此类的方法。
截止目前(2023年1月),Rebuffi等人提出的融合数据增强方法仍是领域内最优的对抗防御方法。开源对抗鲁棒性排行榜 RobustBench 1 的统计结果显示,生成模型加CutMix再加上更宽的模型(WideResNet-70-16)可以在标准数据集CIFAR-10上取得66.11%的对抗鲁棒性和88.74%的干净准确率,大大超出此前的所有防御方法。相信在后续的研究中,不借助外部数据的数据增广技术会成为取得更优对抗鲁棒性的必备技巧。
7.3.6. 参数空间对抗训练¶
对抗训练通过在对抗样本上训练模型使其输入损失景观(input loss landscape)变得平坦。与前面的方法不同,Wu等人 (Wu et al., 2020) 研究了模型的权重损失景观(weight loss landscape)与对抗训练之间的关联,发现损失景观的平坦程度与自然和鲁棒性泛化之间的相关性,并指出一些对抗训练的改进技术,如早停(early stopping)、新损失函数、增加额外数据等,都隐式地让损失景观变得更平坦。
基于上述发现,Wu等人提出了对抗权重扰动(adversarial weight perturbation,AWP)对抗训练方法,在对抗训练过程中通过显式的约束损失景观的平坦度来提高鲁棒性。AWP方法交替对输入样本和模型参数进行对抗扰动,在对抗训练框架下形成了一种双扰动机制。 AWP的优化框架定义如下:
其中,\(v \in \mathcal{V}\)是对模型参数的对抗扰动,\(\mathcal{V}\)是可行的扰动区域;相应的\(r\)是对输入样本的对抗扰动,\(\| r\| \leq \epsilon\)是其可行的扰动区域。借鉴输入扰动的大小限定,参数空间的扰动可以限定为:\(\| v_l\| \leq \gamma\|\theta_l\|\),其中\(l\)表示神经网络的某一层。这种按照缩放比例的上界限定主要是考虑不同层之间的权重差异交大,且权重具有隔层缩放不变性(前一层放大后一层缩小就等于没有改变)。在具体的训练步骤方面,AWP先使用PGD算法构造对抗样本\(x_{\text{adv}} = x + r\),然后使用对抗最大化技术对模型参数生成扰动\(v\),最后计算损失函数\(\mathcal{L}(f_{\theta + v}( x+ r),y)\)对于扰动后的参数\(\theta+ v\)的梯度并更新模型参数\(\theta\)。
实验表明,AWP确实会带来更平坦的损失景观和更好的鲁棒性,认证了显式的约束损失景观的重要性。AWP可以和已有对抗训练方法,如PGD对抗训练、TRADES等相结合,进一步提升他们的鲁棒性。然而,AWP对抗训练是一个min-max-max三层优化框架,会在普通对抗训练的基础上继续增加计算开销。
7.3.7. 对抗训练的加速¶
对抗训练比普通训练多了一个内部最大化过程,需要多次反向传播,大大增加了计算开销。对抗训练的效率问题制约着其在大数据集上的应用,也难以与大规模预训练方法结合训练对抗鲁棒模型。近年来,对抗训练加速方面的研究工作已有不少,但在提升效率的同时都或多或少会牺牲一部分鲁棒性。现有方法大都通过两种思想来加速对抗训练:(1)提高对抗梯度的计算效率;(2)减少内部最大化的步数。
直观来讲,对抗梯度(对抗损失到输入样本的梯度)的计算需要沿着整个神经网络进行反向传播直至输入层,是其主要的效率瓶颈。为了解决此问题,对抗梯度加速计算方法通过巧妙的复用模型参数更新的梯度(模型梯度)来估计对抗梯度(输入梯度),从而达到避免每次计算对抗梯度都需要一次单独的、完整的反向传播的问题。此外,对抗训练(如PGD对抗训练)往往需要多步优化方法来解其内部最大化问题,所以如果能够在更少的步数内有效解决此问题也可以达到加速的目的。而减少内部最大化的步数也就自然而然的成为一种经典的对抗训练加速方法。下面我们将对四种经典的加速方法进行详细的介绍。
Free对抗训练。 Shafahi等人 (Shafahi et al., 2019) 在2019年提出Free对抗训练方法,通过重使用模型更新(外部最小化)的梯度信息来近似对抗梯度(内部最大化),以此来降低内部最大化所带来的计算开销。具体来说,Free对抗训练提出了两个巧妙的加速技巧。首先,损失到输入的梯度与损失到神经网络第一个隐层的梯度是关联的,也就是说,我们可以在正常梯度后传的基础上多传一层从第一个隐层传到输入层就可以同时得到损失到模型参数和输入的梯度。其次,上述的技巧对一次模型梯度后传只会得到一个对抗梯度,也就是只能完成一步攻击。那么如何解决多步攻击的问题呢?作者提出巧妙的利用模型更新跟对抗攻击的步数比例(即1:1,一次模型更新完成一步攻击)在m次模型更新的同时完成m步的攻击。所以我们需要修改模型的训练策略,在一个训练周期中,传统的训练方法在一批数据上更新一次模型然后换到下一批数据,而Free对抗训练在同一批数据上更新模型\(m\)次(并同时生成\(m\)步对抗攻击),然后再换到下一批数据。如此一来,通过调整模型的训练策略,我们可以即完成模型的正常训练又能大幅提高对抗梯度的计算效率。
Free对抗训练的详细训练步骤可参考算法 图7.3.2 。 其首先将其训练的总周期(epoch)数除以\(m\),以保证总体的训练迭代次数和普通对抗训练一致。在训练中,对于每一个批次的数据,循环\(m\)次,每一次反向传播一次,得到参数\(\theta\)的梯度\(\nabla_{\theta}\)和对于输入\(x\)的梯度\(\nabla_{ x}\),最后分别将二者更新到模型参数上和样本\(x\)上,达到同时训练模型和构造对抗样本的目的。
Free对抗训练在 CIFAR-10等较小的数据集上能以极小的额外成本实现与10步PGD(PGD-10)对抗训练相当的鲁棒性,并且可以达到7-30倍的训练加速 (Shafahi et al., 2019) 。Free对抗训练是较早利用模型更新过程中的梯度信息来加速对抗训练的工作,不过由于Free对抗训练需要对传统的模型训练步骤进行较大的改变,且改变后的训练策略在不同学习任务下的性能不确定,这在一定程度上阻碍了该算法的广泛应用。

图7.3.2 Free对抗训练(Free-m)¶
YOPO对抗训练。 同在2019年,Zhang等人 (Zhang et al., 2019) 提出了YOPO对抗训练加速方法。与Free对抗训练一样,YOPO提出巧妙的复用模型参数梯度信息来估计对抗梯度信息,但与Free不同的是,YOPO并不需要修改模型的整体训练策略。根据链式法则,损失到输入的梯度可以进行如下的分解:
其中,\(f^1\)表示神经网络的第一层(第一个隐藏层)。上述分解表明损失对输入的梯度等于损失对模型第一层的梯度乘以第一层对输入的梯度。所以一个\(m \times n\)的PGD对抗训练(PGD-\(m \times n\))可以被分解为\(m\)次损失对第一层的梯度\(\nabla_{f^1}\mathcal{L}(f( x),y)\)乘以\(n\)次第一层到输入的梯度\(\nabla_{ x}f^1( x)\)。通过如此分解,可以将计算消耗降低为原来的\(\frac{m}{mn}=\frac{1}{n}\)(这里假设\(\nabla_{ x}f^1\)的计算消耗可以忽略不计)。由于原论文中的计算过程比较复杂,我们在此进行了化简,化简后的训练步骤参考算法 图7.3.3 。

图7.3.3 YOPO对抗训练(YOPO-m-n)¶
上述算法是基于梯度的YOPO算法,此外作者基于最优控制理论中的庞特里亚金最大化原理(Pontryagin’s maximum principle,PMP)对此算法进行了进一步泛化,使其适用于梯度下降以外的更广泛的优化算法(如离散时间微分博弈问题)。 YOPO可达到跟现有对抗训练方法如PGD对抗训练和TRADES类似的性能,并能带来4-5倍的训练加速。
Fast对抗训练。 与上述加速方法不同,Wong等人 (Wong et al., 2020) 提出通过缩减生成对样本的步数以及配合其他训练加速技巧来加速对抗训练。首先,Wong等人发现在内部最大化过程中可以使用单步PGD算法(即FGSM算法加随机对抗噪声初始化)来代替多步的PGD算法,以此来降低多步对抗训练的计算成本。值得一提的是,单步对抗训练长期以来被认为是无效的(因为其无法防御多步攻击)。对此,Wong等人探索发现问题在于单步训练在\(\epsilon\)-球面附近的过拟合,随机对抗噪声初始化可以有效缓解此问题。值得注意的是,其在CIFAR-10的随机初始化很大,在达到了\(\epsilon=10/255\)。由此得到的单步对抗训练方法可以媲美多步训练方法。在此基础上,可以结合周期学习率调整(cyclic learning rate) (Smith and Topin, 2018) 、混合精度训练(mixed-precision training) (Micikevicius et al., 2018) 和早停(early stopping)进一步提高对抗训练的效率。此外,在大规模、高分辨率数据集ImageNet上,Fast将训练分为三个阶段,分别使用不同的分辨率进行训练。
Fast算法对对抗训练的效率提升是巨大的,其可以在12个小时内完成在ImageNet数据集上的训练(\(\epsilon=2/255\)),而在CIFAR-10数据集上则可以在6分钟之内完成(\(\epsilon=8/255\))。此效率与Free对抗训练相比也有5-6倍的加速。虽然加速效果显著,但Fast对抗训练依赖精细的超参数调整(比如学习率),并不能容易的扩展到其他数据集上。例如,在新数据集上寻找最优的动态学习率调整策略对Fast来说是一个巨大的挑战,大部分情况下需要基于多次重训练探索得到,无形之中反而增加了计算消耗。此外,Fast对抗训练与标准的对抗训练方法相比,鲁棒性有一定程度的下降(虽然比其他加速方法已经好很多了)。抛开这些不足,Fast对抗训练的提出对大规模高效对抗训练起到了极大的推动作用。
周期迁移对抗训练。 Zheng等人 (Zheng et al., 2020) 发现在对抗训练过程中,来自两个相邻周期的模型之间存在较高的对抗迁移性,即前一个周期生成的对抗样本在之后的周期里依然具有对抗性。利用这一特性,Zheng等人提出了基于迁移对抗样本的对抗训练(adversarial training with transferable adversarial examples,ATTA)方法,利用周期可迁移对抗样本来累积对抗扰动,减少后续周期中生成对抗样本所需的扰动步数,从而达到加速训练的目的。ATTA算法在上一个训练周期里存下生成的对抗噪声以及随机剪裁或补齐的偏移量,然后在下一个训练周期中利用存下的对抗噪声进行攻击初始化,如此往复,直到模型训练结束。实验表明,ATTA可以在MNIST和CIFAR-10等小数据集上对PGD对抗训练达到12-14倍的加速,且能带来小幅的鲁棒性提升。虽然ATTA方法减少了对抗样本的构造时间,但是其需要存储大量的中间样本,带来了额外的数据I/O开销。此外,ATTA方法对数据增广比较敏感,由于两个周期之间存在增广随机性,所以需要针对数据增广做噪声对齐,也就很难应对复杂的数据增广算法,如Mixup和Cutout等。
7.3.8. 大规模对抗训练¶
作为一种双层优化方法,对抗训练需要消耗高于普通训练数倍的算力。粗略估计,在ImageNet数据集上进行对抗训练需要消耗相当于小数据集CIFAR-10的1000倍算力,给开展相关实验带来巨大挑战。此外,ImageNet上的普通训练本身就比在CIFAR-10等小分辨率数据集上更加难收敛,带来进一步的挑战。这些挑战制约了对抗训练在大规模数据集上的研究,导致相关研究相对较少。由于大规模对抗训练可以提供鲁棒的预训练模型,大大推动领域的发展,所以我们在这里着重介绍几个在大规模对抗训练方面的研究工作。
实际上,早在2016年Kurakin等人 (Kurakin et al., 2016) 就在此方面进行了一定的研究。他们发现对抗训练中干净样本和对抗样本最好是进行1:1的配比(一半干净样本一半对抗样本),每个样本的扰动上限\(\epsilon\)最好是在一定范围内随机指定(而非固定不变)。经过对应的改进,Kurakin等人在ImageNet数据集上使用单步FGSM对抗训练成功的训练了一个Inception v3模型。但是我们知道,单步对抗训练所带来的的鲁棒性是有限的。此外,上述介绍的对抗训练加速方法(如Fast)也基本都在ImageNet数据集上进行了认证,因为加速的主要目的是让大规模对抗训练成为可能。但是由于加速本身往往让精确的对抗梯度计算变为近似,所以鲁棒性往往达不到标准(未加速)对抗训练的水平。 目前,在ImageNet上的标准对抗训练工作主要包括Xie等人的特征去噪对抗训练(feature denoising adversarial training,FDAT) (Xie et al., 2019) 、Qin等人的局部线性正则化训练(local linearity regularization,LLR) (Qin et al., 2019) 、Xie等人的平滑对抗训练(smooth adversarial training) (Xie et al., 2020) 等。
特征去噪对抗训练。 特征去噪的概念与输入去噪类似,不过是在特征空间进行,通过一些过滤操作将对抗噪声在特征空间中移除掉。在FDAT工作中,Xie等人测试了四种去噪操作(在残差网络的残差块之后添加),包括非局部均值(non-local mean) (Buades et al., 2005) 、双边滤波器(bilateral filter)、均值滤波器(mean filter)和中值滤波器(median filter)。其中,非局部均值去噪操作的定义如下:
其中,\(f^l\)表示神经网络第\(l\)层的特征输出;\(\omega\)是与特征\(f^l_i\)和\(f^l_j\)相关的权重函数;特征\(f^l_i\)和\(f^l_j\)对应特征图上的两个位置;\(\mathcal{C}(f^l)\)是一个归一化函数;\(\mathcal{S}\)表示整个特征空间(所有维度集合)。上式是对\(i\)-维特征做全局的加权特征融合。Xie等人发现基于softmax加权平均的非局部均值操作可以带来最优的鲁棒性,加权函数定义如下:
其中,\(\Phi_1\)和\(\Phi_2\)是特征的两个嵌入版本(通过两个\(1 \times 1\)的卷积操作获得);\(d\)是通道个数;\(\mathcal{C}(f^l)= \sum_{\forall j \in \mathcal{S}} \omega(f^l_i,f^l_j)\);\(\omega(f^l_i,f^l_j)/\mathcal{C}(f^l_i)\)则为softmax函数。
通过进一步将特征去噪与PGD对抗训练结合,Xie等人将ImageNet上的PGD-10鲁棒性从27.9%(Kannan等人提出的对抗逻辑匹配方法(ALP) (Kannan et al., 2018) )提高到了55.7%,在防御2000步的PGD攻击(PGD-2k)时也取得了42.6%的鲁棒性。特征去噪对抗训练赢得了CAAD (competition on adversarial attacks and defenses)2018的冠军,是大规模对抗训练领域一个重要的工作。
局部线性正则化。 Qin等人 (Qin et al., 2019) ,提出局部线性正则化(LLR)对抗训练方法,通过显式的约束训练样本周围的损失景观使其更线性化,以此来避免对抗训练中存在的梯度阻断(gradient obfuscation)问题。LLR对抗训练与常规对抗训练算法不同,定义如下:
其中,\(\gamma( \epsilon, x)=|\mathcal{L}_{\text{CE}}(f( x+ r_{\text{LLR}}),y) - \mathcal{L}_{\text{CE}}(f( x),y) - r_{\text{LLR}}^{\top}\nabla_{ x}\mathcal{L}_{\text{CE}}(f( x),y) |\)基于损失在样本\(x\)附近的泰勒展开定义了\(x\)周围损失景观的线性程度;\(r_{\text{LLR}}=\mathop{\mathrm{arg\,max}}_{\| r\|_p \leq \epsilon} |\mathcal{L}_{\text{CE}}(f( x+ r_{\text{LLR}}),y) - \mathcal{L}_{\text{CE}}(f( x),y) - r_{\text{LLR}}^{\top}\nabla_{ x}\mathcal{L}_{\text{CE}}(f( x),y) |\)是\(x\)周围最坏情况的扰动(即对抗扰动);\(\lambda\)和\(\mu\)是两个超参数。其中,涉及到\(r_{\text{LLR}}\)的部分仍然需要PGD攻击算法求解,但是需要的步数比PGD对抗训练更少(比如两步PGD),为了帮助线性正则化,激活函数也由ReLU替换成了softplus函数(\(\log(1 + \exp(x))\)) (Nair and Hinton, 2010) 。Qin等人实验展示了LLR对抗训练的有效性,在ImageNet上对无目标PGD攻击的鲁棒性达到了47%(\(\epsilon=4/255\)),而此鲁棒性也在AutoAttack的评估实验中得到了确认 (Croce and Hein, 2020) 。
平滑对抗训练。 此外,Xie等人 (Xie et al., 2020) 还研究了激活函数对对抗鲁棒性的影响,发现普遍使用的ReLU激活函数并不利于对抗鲁棒性,而训练更鲁棒的神经网络需要更平滑的激活函数。基于此,他们提出了平滑对抗训练(smooth adversarial training,SAT)方法,对ReLU激活函数进行平滑近似,即将ReLU替换为softplus (Nair and Hinton, 2010) 、SILU (Ramachandran et al., 2017) 、GELU (Gaussian Error Linear Unit) (Hendrycks and Gimpel, 2016) 和ELU(Exponential Linear Unit) (Clevert et al., 2016) 。其中,SILU取得了最优的鲁棒性,其定义如下:
通过简单的激活函数替换,SAT几乎以“零代价”提高了对抗鲁棒性,而且对小模型和大模型都适用,在ImageNet上训练大模型EfficientNet-L1 (Tan and Le, 2019) 取得了58.6%的鲁棒性。值得注意的是这里的对抗训练使用的是单步的Fast对抗训练,扰动上限为\(\epsilon=4/255\)。
7.3.9. 对抗蒸馏¶
知识蒸馏 (Hinton et al., 2015) 是一种广泛使用的性能提升技术,其主要思想是借助教师模型(一般是大模型)来提升学生模型(一般是小模型)的泛化性能,往往优于从头训练学生模型。知识蒸馏技术已被应用于对抗防御,一方面用来提升模型的对抗鲁棒性,另一方面用来更好的进行准确率-鲁棒性权衡。此外,对抗训练往往需要更大的模型,这制约了其在资源受限场景下的应用,因此如何使用鲁棒预训练的大模型蒸馏得到鲁棒的小模型也是一个研究热点。
虽然Papernot等人 (Papernot et al., 2016) 早在2016年就提出了“防御性蒸馏”(defensive distillation)的概念,但是这并不是基于知识蒸馏的防御。防御性蒸馏是一种模型后处理(post-processing)技术,将模型输出逻辑值的数量级变大,以此来让其对微小输入变化不敏感。防御性蒸馏所得到的模型仍然可以被适应性攻击绕过 (Carlini and Wagner, 2016) 。下面介绍两个真正基于知识蒸馏的对抗蒸馏方法。
对抗鲁棒蒸馏。Glodblum等人 (Goldblum et al., 2020) 研究了在知识蒸馏过程中对抗鲁棒性从教师模型向学生模型迁移的过程,发现当一个模型具有鲁棒性时,仅仅利用自然样本进行蒸馏便可训练出具有一定鲁棒性的学生模型。基于此,Glodblum等人提出对抗鲁棒蒸馏 (adversarially robust distillation, ARD)的概念,将具有教师模型的对抗鲁棒性迁移到学生模型。ARD优化框架定义如下:
其中,\(T( x)\)和\(S( x)\)分别为教师和学生模型;\(x_{\text{adv}}\)为\(x\)的对抗样本,\(\tau\)为蒸馏温度,\(\alpha\)为平衡准确率和鲁棒性的超参数。
上式中,第一个损失项是在干净样本上定义的分类损失项,第二项为鲁棒性蒸馏损失项。其中在内部最大化过程中,ARD依然使用PGD算法配合交叉熵损失函数\(\mathcal{L}_{\text{CE}}\)来生成对抗样本。作者猜测对抗鲁棒性蒸馏不仅可以使学生网络具有高精度的自然准确率还会有较好的鲁棒性,实验结果也证实了这一猜测,学生模型的鲁棒性和自然准确率都超过了同样架构的模型 (Goldblum et al., 2020) 。
鲁棒性蒸馏。Zi等人 (Zi et al., 2021) 将PGD对抗训练、TRADES、MART等都看做是一种自蒸馏(单模型,自己蒸馏自己)的训练方式,并结合ARD算法等发现了一个鲁棒性规律:当训练方法使用的是鲁棒软标签(鲁棒模型的概率输出)时,其鲁棒性往往要优于使用硬标签的方法。基于此发现,Zi等人提出鲁棒软标签对抗蒸馏方法(robust soft label adversarial distillation,RSLAD),使用鲁棒教师模型的概率输出来提高学生模型的鲁棒性。RSLAD训练解决下列优化问题:
其中,\(T( x)\)和\(S( x)\)分别是教师和学生模型;算法通过固定\(\tau=1\)取消了蒸馏温度超参。与ARD不同,RSLAD使用KL散度损失来生成对抗样本,相当于将ARD基于硬标签的交叉熵损失替换成了基于软标签的KL散度。类似的,RSLAD的外部最小化也将两个损失项(分类损失和蒸馏损失)全部替换成了KL散度。 实验表明,使用RSLAD可以使得学生模型获得良好的鲁棒性和泛化力。此外,Zhu等人 (Zhu et al., 2021) 提出内省对抗蒸馏方法(introspective adversarial distillation,IAD)使学生模型有选择性的信任教师模型输出的软标签。
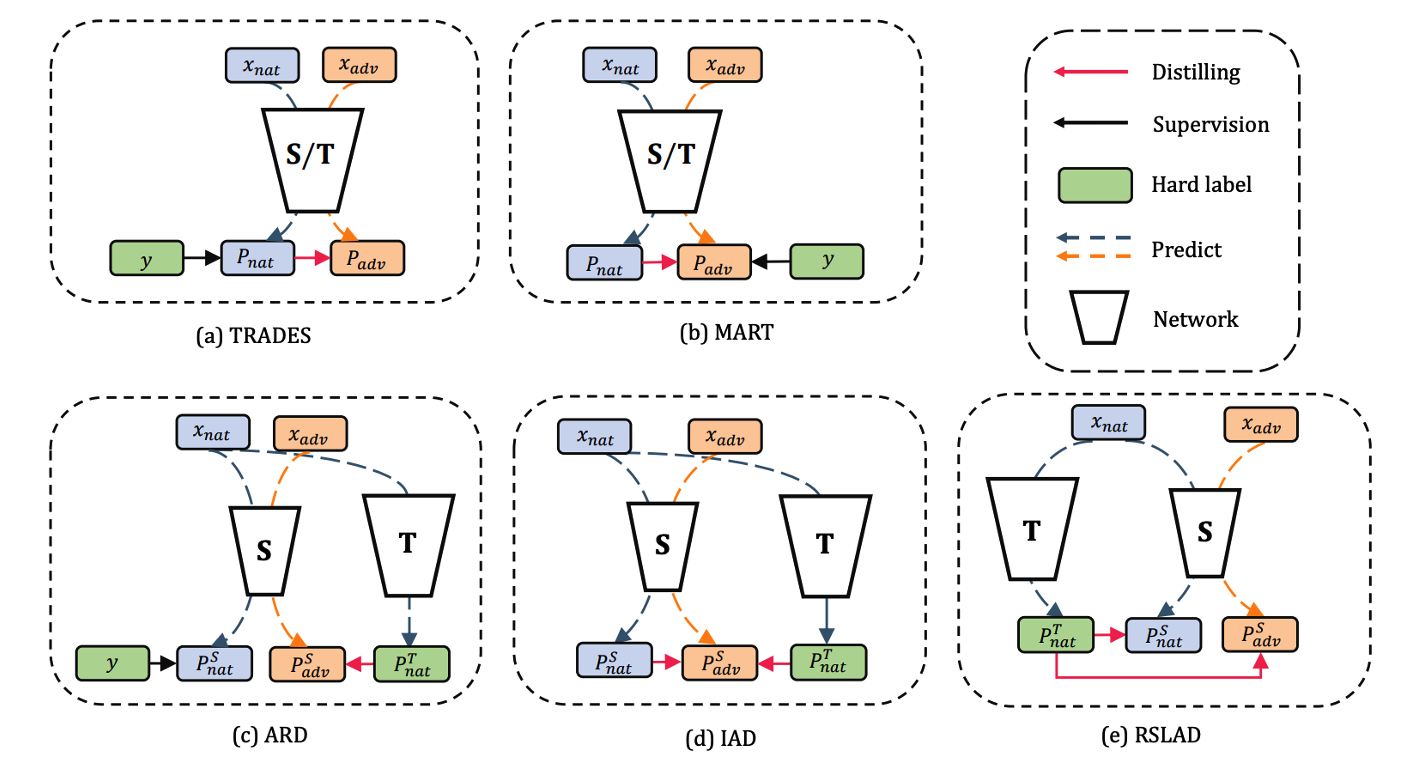
图7.3.4 从对抗鲁棒性蒸馏的角度来看对抗训练算法TRADES、MART以及蒸馏算法ARD、IAD和RSLAD。¶
图 图7.3.4 从对抗鲁棒性蒸馏的角度分析比较了不同算法所使用的监督信息(软标签还是硬标签),以及自然样本和对抗样本在整个蒸馏框架中的不同参与方式。总体来说,对抗蒸馏方法需要一个鲁棒预训练的大教师模型,可惜的是受制于对抗训练的效率瓶颈,目前领域内可用的鲁棒大模型很少,这阻碍了对抗蒸馏技术的进一步发展。
7.3.10. 鲁棒模型结构¶
最完美的对抗防御莫过于模型结构本身就具有天然对抗鲁棒性,这是安全人工智能所追求的终极目标。可惜的是,大量实验表明这样的模型结构是不存在的。我们可以从对抗样本成因部分(章节 7.1节 )看到,深度学习模型存在巨大的对抗脆弱性,显然不符合鲁棒模型结构的要求。这一度让研究者们非常困惑,甚至认为深度学习模型并不能带来真正的智能,因为真正的智能最起码应该对微小的输入扰动鲁棒。这激发了我们对鲁棒模型结构的持续探索。鲁棒结构探索不但对对抗防御有重要的意义,甚至可能会给人工智能领域带来变革。
截至目前,我们至少知道经过对抗训练的模型是具有一定鲁棒性的。所以当前关于鲁棒模型结构的探索大都是基于对抗训练完成的,即寻找对抗训练后更鲁棒的模型。在对抗训练方法的探索过程中,研究者发现使用更宽的深度神经网络往往能带来更好的对抗鲁棒性 (Madry et al., 2018) ,比如相较普通残差网络(ResNet-18或者ResNet-34),10倍宽的WideResNet(WideResNet-28-10或者WideResNet-34-10)在对抗训练后要更鲁棒。这一观察也使得后续的对抗训练方面的工作都倾向于使用更宽的模型 (Wang et al., 2019, Wang et al., 2019, Zhang et al., 2019) ,目前最优的对抗训练方法甚至使用了16倍宽的WideResNet-70-16 (Rebuffi et al., 2021) 。此外,Cazenavette等人 (Cazenavette et al., 2021) 研究发现残差网络中使用的跳连(Skip Connection)结构对提高更深模型的对抗鲁棒性比较重要。
实际上,关于是否更宽(或更大)的模型会更鲁棒的问题目前仍然没有确定的答案。比如有些工作发现简单的按照一定比例对网络进行宽度或者深度的放大并不一定会带来更多的鲁棒性 (Nakkiran, 2019, Su et al., 2018) 。Wu等人 (Wu et al., 2021) 发现并不是更宽的网络会更鲁棒,反而会在扰动稳定性(perturbation stability)方面要差于普通网络,导致更差的鲁棒性,不过可以通过宽度调整正则化(width adjusted regularization)来解决。
Huang等人 (Huang et al., 2021) 通过精细化控制WideResNet神经网络的宽度和深度比例,探索了神经网络结构对对抗鲁棒性的影响,发现简单的加深或者加宽网络并不一定能带来更鲁棒的结构,而网络的深层块(deep blocks)越窄或者越浅在对抗训练后鲁棒性越好。Huang等人还发现了残差神经网络结构中深度和宽度的黄金比例,并认证了此黄金比例也适用于WideResNet以外的网络结构,如VGG、DenseNet、神经网络结构搜索(nerual architecture search,NAS)到的结构 等。
说到鲁棒模型结构我们就不得不提基于神经网络结构搜索的方法。Guo等人 (Guo et al., 2020) 基于单样本NAS(one-shot NAS) (Bender et al., 2018) 以及PGD对抗训练对鲁棒神经网络结构进行了搜索,发现:
密集连接(densely connected)的单元有利于提高模型的对抗鲁棒性;
在给定的计算预算下,向直连边(direct connection edge)添加卷积操作会提高对抗鲁棒性。
后续的工作通过不同的方式改进了此方法。Ning等人 (Ning et al., 2020) 指出单样本NAS会倾向于在超网络中选择容量更大的网络结构,并通过多样本NAS(multi-shot NAS)改进了Guo等人提出的方法,在特定容量预算下可以搜索到更鲁棒的网络结构。Chen等人 (Chen et al., 2020) 提出ABanditNAS(anti-bandit NAS)方法,对去噪模块、无参操作、Gabor滤波器以及卷积进行了搜索,并利用置信区间上界(upper confidence bound,UCB)丢弃臂(arm)来提高搜索效率,同时利用置信区间下界(lower confidence bound,LCB)促进不同臂之间的公平竞争。该方法取得了更快的搜索速度和更鲁棒的模型。Hosseini等人 (Hosseini et al., 2021) 定义了两个鲁棒性度量,即认证下界(certified lower bound)和雅可比范数下界(Jacobian norm bound),并基于DARTS(differentiable neural architecture search) (Liu et al., 2019) 最大化两个鲁棒度量来搜索鲁棒网络结构。DARTS可以说是最经典的可微神经网络结构搜索算法。相比之前的方法,Hosseini等人提出的方法在搜索过程中显式的进行了鲁棒性搜索,所以可以得到更鲁棒的结构。
上面提到的鲁棒结构搜索方法大都基于对抗训练进行。但是对抗训练计算开销很大,很难与NAS技术结合进行充分的搜索。从另一个角度来讲,即使基于全量的对抗训练也无法保证搜索出来的模型就一定比手工设计的模型更鲁棒。Devaguptapu等人 (Devaguptapu et al., 2021) 就对NAS得到的模型结构和手工设计的结构进行了比较,发现在不使用对抗训练的情况下,基于DARTS的随机采样和简单集成是可以搜索到具有一定鲁棒性的模型结构的;但是NAS得到的模型结构只在简单任务和数据集上比手工设计的模型更鲁棒一些,放在复杂的任务和数据集上就不行了。
总体来说,基于NAS的鲁棒模型结构搜索主要面临两个方面的挑战:(1)搜索空间的设计;(2)对抗训练的高计算开销。这两个挑战制约了当前NAS鲁棒结构搜索方法,在未来或许能在这两个方面取得一定的突破,比如基于单步对抗训练的搜索或者在已有鲁棒模型的基础上做结构扩展 (Li et al., 2021) 。
近年来,视觉Transformer(Vision Transformer,ViT)模型逐渐流行,不断推高视觉任务的最佳性能 (Dosovitskiy et al., 2021, Liu et al., 2021) 。关于ViT模型的对抗鲁棒性,领域内已有一些研究。Bhojanapalli等人 (Bhojanapalli et al., 2021) 以及Shao等人 (Shao et al., 2021) 发现ViT模型比普通CNN要更鲁棒一些。然而,Mahmood等人 (Mahmood et al., 2021) 和Bai等人 (Bai et al., 2021) 分别指出前面的分析工作并不公平,因为参与比较的ViT模型往往比普通CNN要大很多,如果在同等参数量的前提下进行比较的话,ViT模型并不比普通CNN更鲁棒。
Tang等人 (Tang et al., 2021) 对现有深度神经网络模型进行了大规模鲁棒性评估,包括49个手动设计的模型、1200多个NAS得到的模型以及10多种训练技巧。实验发现,在同等模型大小和训练设置下,在对抗鲁棒性方面不同类型的模型排行为:Transformers > MLP-Mixers > CNNs;而在应对自然和系统噪声方面:CNNs > Transformers > MLP-Mixers。不过对抗训练得到的模型可以应对所有噪声类别。对于一些轻量级模型来说,简单的增大模型或者增加额外训练数据并不能提升其鲁棒性。相信随着模型种类越来越丰富,我们可以通过类似的大规模研究探寻到构建鲁棒模型结构的基本原则,并基于此逐步设计越来越鲁棒、越来越安全的模型。
7.4. 输入空间防御¶
除了前面介绍的几种主流防御方法以外,近年来也陆续提出了一些输入空间的防御方法,包括输入去噪、输入压缩、输入随机化等。本小节简单介绍六种这方面的防御方法。需要注意的是,此类方法的真实鲁棒性还有待认证,一些攻击工作,如BPDA (Athalye et al., 2018) ,发现输入去噪方法仍然可以被绕过。
7.4.1. 输入去噪¶
Liao等人 (Liao et al., 2018) 提出高级表征去噪器(high-level representation guided denoiser, HGD)防御来应对图像分类模型的对抗攻击。HGD算法通过最小化对抗样本与自然样本之间的去噪输出差距来达到移除对抗噪声的目的。在去噪模型方面,作者使用U-net结构 (Ronneberger et al., 2015) 改进了自编码器,并提出了去噪U-net模型(DUNET)。在损失函数方面,作者使用模型在第\(l\)层的特征输出差异作为损失函数:\(\mathcal{L}=\|f^l( x_{\text{rec})-f^l( x)}\|\),其中\(x_{\text{rec}}\)是重建样本。根据第\(l\)层的不同选择,又可以分为像素指导去噪(pixel guided denoiser)、特征指导去噪(feature guided denoiser)、逻辑指导去噪(logits guided denoiser)以及 类别标签指导去噪(class label guided denoiser),其中后三种去噪损失中的监督信息来自于模型深层的高级表征,所以统称为HGD。在这四种去噪方法中,作者发现逻辑指导去噪防御方法可以更好的权衡自然准确率和对抗鲁棒性。
7.4.2. 输入压缩¶
Das等人 (Das et al., 2017) 使用JPEG压缩作为一种数据预处理的对抗防御技术。其主要思想是:JPEG压缩可以移除图像局部区域内的高频信息,这样的操作有助于去除对抗噪声。除此之外,作者还提出了一种集成算法,可以防御多种对抗攻击。JPEG压缩防御的特点为:(1)计算快,不需要去噪模型;(2)不可微,可以阻止基于反向传播的适应性对抗攻击。 Jia等人 (Jia et al., 2019) 提出端到端的图像压缩模型ComDefend来防御对抗样本,其主要由两部分组成:(1)压缩卷积神经网络(ComCNN)和(2)重建卷积神经网络(RecCNN)。 其中,ComCNN用于获得输入图像的结构化信息并去除对抗噪声,而RecCNN则用于重建原始图像。ComDefend防御方法的特点是:(1)可以保持较高的自然准确率和不错的鲁棒性;(2)可以与其他防御方法结合,进一提高模型的鲁棒性。
7.4.3. 像素偏转¶
由于图像分类模型往往对自然或随机噪声鲁棒,因此Prakash等人 (Prakash et al., 2018) 提出像素偏转(pixel deflection)方法,通过重新分配像素值强制输入图像匹配自然图像的统计规律,从而可以利用模型自身的鲁棒性来抵御对抗攻击。具体的操作步骤为:
生成输入图像的类激活图(class activation map,CAM),也称注意力图;
从图像中采样一个像素位置\(( x_1, x_2)\),并获得该像素的归一化激活图值;
从均匀分布\(\mathcal{U}(0, 1)\)中随机采样一个值;
如果归一化激活图值低于采样的随机值,则进行像素偏转。
重复上述操作\(K\)次,可以得到一个破坏了对抗噪声的图像。此外,通过以下步骤对破坏了对抗噪声的图像进行恢复:(1)将图像转换为\(YC_{b}C_{r}\)格式;(2)使用离散小波变换将图像投影到小波域中;(3)使用BayesShrink (Chang et al., 2000) 对小波进行软阈值处理;(4)计算收缩小波系数的逆小波变换;(5)将图像转回RGB格式。像素偏转防御方法对简单的对抗攻击比较有效,但不能防御更强大的对抗攻击。
7.4.4. 输入随机化¶
Xie等人 (Xie et al., 2018) 提出推理阶段对抗防御方法,通过两种随机化操作打破对抗噪声的干扰:(1)随机大小调整,将输入图像调整为随机大小;(2)随机填充,以随机方式在输入图像周围填充零。 实验表明,所提出的随机化方法在防御单步攻击和迭代攻击方面非常有效。 此方法具有以下优点:(1)无需额外的训练或微调;(2)很少有额外的计算;(3)可与其他对抗性防御方法兼容。 具体来说,首先将输入图像\(x\)由大小\(W\times H \times3\)缩放至\(W'\times H'\times 3\),同时保证缩放后的尺寸在一个合理的范围内;然后将缩放后的图像随机补零,使其尺寸达到\(W”\times H”\times3\);最后使用变换后的图像进行推理。此防御方法可以简单有效的抵御大多数对抗攻击,但不能防御后续提出的一些更强大的攻击方法。
7.4.5. 生成式防御¶
Samangouei等人 (Samangouei et al., 2018) 提出基于对抗生成网络的 Defense-GAN防御方法,利用生成模型的超强表达能力来保护深度神经网络免受对抗攻击。Defense-GAN的思想也很直观,使用GAN生成的自然样本来代替可能是对抗样本的测试样本来进行推理。其首先训练一个生成器\(G\),以随机向量为输入,输出自然样本;然后在推理阶段通过采样不同的随机向量生成一批“自然”样本,通过寻找与测试样本最近的生成样本进行推理。得到的生成器可服务于相同任务上的任意分类模型,且可以与其他防御方法相结合。但是由于此方法要单独训练一个生成器,所以需要消耗大量的算力。 由于Defense-GAN是高度非线性的,所以可以防御白盒攻击,但仍可以被梯度估计或者黑盒攻击绕过。 Shen等人 (Jin et al., 2019) 提出基于自动编码器的对抗噪声消除GAN(adversarial perturbation elimination GAN, APE-GAN),此方法将对抗样本复原成干净样本,然后将复原的样本输入神经网络进行分类。值得一提的是,APE-GAN的生成器并不鲁棒,虽然在攻击者不知道生成器的存在的情况下可以防御简单的攻击,但是一旦生成器暴露则无法适应性攻击。
7.4.6. 图像修复¶
Gupta等人 (Gupta and Rahtu, 2019) 采用图像修复(image inpainting)的思想对输入图像的关键区域进行重建和去噪,以此来达到去除对抗噪声的目的。其中,修复区域可以基于几个排名靠前类的类激活图(CAM) (Zhou et al., 2016) 结合一个输入掩码进行定位。此方法被命名为CIIDefence(class specific image inpainting defence)。在图像修复之前,CIIDefence还进行了小波去噪操作,因为修复操作容易导致模型的注意力向非修复区域转移,这些区域也同样需要防御。为了进一步阻断反向传播,作者将小波去噪和图像修复组合成一个不可微的层。值得注意的是,图像修复模型也是一个GAN。实验表明,CIIDefence也可以正确识别经过不同攻击算法产生的对抗样本,还可以有效的防止BPDA等近似攻击方法。与此同时,其缺点也十分明显:1)步骤繁琐,需要多步才能完成,耗时较久;2)需要精准选择修复区域;3)对图像的大小有着一定的要求,不适合低分辨率的图像。
7.5. 可认证防御¶
可认证防御(certifiable defense)是相对经验性防御(empirical defense)来说的,其也有时也被称为可证明防御(provable defense)或可验证防御(verifiable defense)等。前文讲的对抗样本检测(章节 7.2节 )、对抗训练(章节 7.3节 )等防御方法都是经验性防御,这些方法可以提供很好的防御效果,但是无法给出严格的鲁棒下界证明。与经验防御不同,可认证防御为模型的对抗鲁棒性提供了严格的理论保证,可以证明输入在一定扰动范围内的输出一致性。若模型对于某个输入样本具有可认证鲁棒性,那么首先模型要正确分类此样本,同时在允许扰动范围内,模型要对所有扰动后的样本也能正确分类。可认证防御保证了模型不会有意外的输出,可以彻底避免一些安全隐患,适用于对安全性要求极高的应用场景。
对深度学习模型进行鲁棒性认证的主要难点在于模型是非线性的,这导致对神经网络的输出进行估计是非常困难的。尽管现在常用的ReLU激活函数的结构已经足够简单,但是研究者已经证明,认证ReLU神经网络的鲁棒性是NP完全问题。这导致很多鲁棒性认证算法由于时间复杂度的限制,难以应用在规模较大的模型上。目前关于鲁棒性认证的研究主要从两个角度展开:一方面,设计精确的认证算法,同时希望此算法可应用于大模型;另一方面,结合特殊的训练方法训练出更容易认证鲁棒性的神经网络。
7.5.1. 基本概念¶
现有鲁棒性认证方法主要基于前馈ReLU神经网络进行。一个\(l\)层的前馈ReLU神经网络\(f_{\theta}\)可形式化如下:
其中\(ReLU( z) = \max\{ z,0\}\),每个\(z_i\)或者\(\hat{ z_i}\)都是在\(\mathbb{R}^n_i\)域上的一个向量,\(W_i\)、\(b_i\)(\(i=2,\ldots,l-1\))是模型参数。
鲁棒性认证(robustness certification)的目标是证明模型在限定空间(扰动范围)内所有输入样本的预测结果的一致性,其形式化定义如下:
其中,\(x_{0}\)为原始输入样本,\(y_{0}\)为样本\(x_{0}\)的真实标签,\(\epsilon\)为\(L_p\)范数下的扰动半径,\(f\)是神经网络模型,\(f( x)\)为模型对输入样本\(x\)的类别预测。
式 (7.5.2) 可以被等价地定义为一个最优化问题 (Li et al., 2023) ,定义如下:
其中,\(y_0\)是输入\(x_0\)的真实标签,\(y_t\neq y_0\)为任意错误类别。需要注意的是,这里大部分认证算法直接取逻辑值作为\(f( x)\)(而不是概率值或者类别预测),因为softmax转换是非线性的,会给认证带来不必要的麻烦。
求解式 (7.5.3) 之后,可以根据下面的条件判断模型在\(L_p\)范数和最大扰动\(\epsilon\)下对样本\(x_0\)的鲁棒性:
从实际应用的角度出发,下面我们将分别介绍认证小模型、中模型和大模型鲁棒性的算法。
7.5.2. 认证小模型¶
基于式 (7.5.1) 可以看出,神经网络对应的函数\(f_{\theta}( x)\)是仿射变换和ReLU运算的顺序组合,而这两种运算都可以用线性不等式与谓词逻辑来刻画。比如,ReLU运算可以表示为:
如此,神经网络可以转换为一组线性不等式定义的逻辑组合,并将鲁棒性认证建模为一个最优化问题(结合式 (7.5.3) ),通过可满足性模理论(satisfiability modulo theories, SMT)求解器来解决。比如,使用\(Z_3\)求解器 (Moura and Bjørner, 2008) 即可求解上述布尔谓词表达式的可满足性,完成鲁棒性认证。
此外,鲁棒性认证问题还可以转换成混合整数线性规划问题(mixed integer linear programming,MILP)进行求解 (Botoeva et al., 2020) 。和线性不等式类似,MILP也可以对神经网络中的运算进行等价转换。相比线性规划,MILP问题可以约束一些变量只取整数而不是实数,这种额外的表达能力使得MILP可以等价转换非线性ReLU操作。比如,对于一个输入可能是正数或者负数的神经元\(z_{i,j}\)来说,其ReLU运算\(z_{i,j} = ReLU(\hat{ z}_{i,j})\)可表示为:
其中,\(l_{i,j}\)是神经元在鲁棒性半径\(\epsilon\)内输出的下界,即\(\min_{ x \in B_{p, \epsilon}( x_0)}\hat{ z}_{i,j}( x)\),\(u_{i,j}\)则是神经元在鲁棒性半径内输出的上界, 即\(\max_{ x \in B_{p, \epsilon}( x_0)}\hat{ z}_{i,j}( x)\),\(a_{i,j}\)是一个在0和1之间取值的整数,当神经元的输入为负值时值为0,当神经元的输入为正时值为1。 因为MILP可以准确对ReLU函数进行编码,所以对神经网络的鲁棒性认证可以转成MILP问题并使用MILP求解器来解决,比如GUROBI求解器 (Gurobi, 2020) 。
上述两种基于精确建模的方法需要结合正则化训练对模型进行鲁棒性认证(否则模型的鲁棒性并不会因为认证算法的存在而改变)。根据Xiao等人的研究 (Xiao et al., 2018) ,以上几种精确鲁棒性认证算法的运行时间与非稳定神经元的数量高度相关。非稳定神经元是指输入可正可负的神经元,而稳定神经元则是指输入恒正或恒负的神经元。基于此理论,Xiao等人提出正则化训练,在训练过程中最小化\(-\tanh(1 + l_{i,j}u_{i,j})\)使ReLU神经元更加稳定,从而增加稳定神经元,降低认证复杂度。其中,\(l_{i,j}\)和\(u_{i,j}\)是神经元\(z_{i,j}\)输出的下界和上界。
对神经网络进行等价转换的鲁棒性认证方法可以精确求解式 (7.5.3) ,得到\(\min_{y_t \neq y_0} \mathcal{M}(y_0,y_t)\),从而判断模型的鲁棒性,这种能够精确求解式 (7.5.3) 的方法被称为完备的认证方法 (Li et al., 2023) 。但是从时间复杂度上来看,求解器的运算过程是NP完全的,所以只适用于小模型。比如,SMT求解器只能认证有数百个神经元的神经网络,MILP求解器虽然可以认证正则化训练的中等规模模型(基于CIFAR-10数据集),但是无法应用于自然(非正则化)训练的小规模模型(基于MNIST数据集)。
ReLU神经网络具有局部线性的特点,一些研究者基于此对网络内部的神经元进行分支,提出了“分支-定界法”。该方法首先使用非完备的认证算法,对式 (7.5.3) 中的\(\mathcal{M}(y_0,y')\)进行定界(如使用线性松弛方法)。如果下界大于0,则神经网络的鲁棒性得到认证,认证结束;若上界小于0,则网络在问题域上没有鲁棒性,认证结束。若上界大于0,下界小于0,则开始进行“分支”操作:递归地选择一个神经元ReLU(\(\hat{ z}_{i,j}\)),分成两个分支:\(\hat{ z}_{i,j} \leq 0\)(分支A)和\(\hat{ z}_{i,j} \geq 0\)(分支B)。分支A的约束为\(\hat{ z}_{i,j} < 0, z_{i,j} = 0\),分支B的约束为\(\hat{ z}_{i,j} \geq 0, z_{i,j} = \hat{ z}_{i,j}\)。可以发现,被拆分神经元只包含线性约束。然后对拆分后的两个分支再次用非完备算法进行定界。重复上述过程,当一条路径的所有的神经元都被拆分后,它将只包含线性约束,此时可以对这条路径实现精确的计算。因为非完备认证方法会比完备认证方法快很多(后面会介绍),所以在定界时使用非完备的认证会加速计算的过程。
由于非完备认证算法有很多选择,且选择不同的神经元进行分支带来的收益也不同,所以定界的方法和分支的策略存在很大的探索空间。对于分支策略,BABSR方法 (Bunel et al., 2020) 有效地估计了每个神经元分支的收益,并选择收益最大的神经元进行分支。FSB方法 (De Palma et al., 2021) 通过模拟每个神经元分支的结果提出了更优的改进估计。对于定界策略,有基于线性上下界传播、区间边界传播、多输入神经元松弛等方法,这些方法都会在下一章节介绍。
基于分支-定界法的\(\alpha\)-\(\beta\)-CROWN认证器 (Wang et al., 2021) 在VNN-COMP 2021比赛中获得第一名。其中CROWN是一个非完备的神经网络认证算法,利用线性不等式进行松弛,并且通过反向的边界传播来估计目标函数的下界。\(\alpha\)-CROWN通过梯度上升来获得更紧的下界。\(\beta\)-CROWN在边界传播过程中结合分支定界法,实现了完备的鲁棒性认证。\(\alpha\)-\(\beta\)-CROWN认证器同时优化了上述两种方法中的\(\alpha\)参数和\(\beta\)参数,取得了更紧的下界。对于经过专门训练的模型,\(\alpha\)-\(\beta\)-CROWN认证器可以在几分钟的时间内认证规模为\(10^5\)个神经元的神经网络,比如在中等规模数据集CIFAR-10上训练的ResNet。而对自然训练的模型,该认证器可以处理\(10^4\)个神经元(大约6层)的神经网络,对应CIFAR-10上的小模型或MNIST上的大模型。
完备的鲁棒性认证方法往往只适用于小模型。对于“等价转换+求解器”类方法来说,未来的研究主要集中在如何找到一个更适合求解器的转换方式以及如何对求解器进行优化。对于“分支-定界法”来说,研究的方向主要有两个:一方面是如何找到一个更有效的非完备认证算法对输出进行定界;另一方面是如何寻找一种新的启发式分支策略,通过尽可能少的分支次数完成认证。此外,近期研究发现一些完备的认证算法在浮点运算下是非完备的,这种漏洞可能会被攻击者利用 (Jia and Rinard, 2021, Zombori et al., 2021) 。所以鲁棒性认证方法还需要考虑浮点数的四舍五入误差,以提高严谨性。
7.5.3. 认证中模型¶
认证更大一些的模型需要降低算法的时间复杂度,比如利用近似算法求出式 (7.5.3) 中\(\mathcal{M}(y_0,y')\)的取值区间。这些近似认证算法也被称为非完备认证算法 (Li et al., 2023) 。直观来讲,可以通过对ReLU函数进行一定的线性松弛来避免求解复杂的MILP问题,提高认证效率。线性松弛的主要思想是利用线性不等式组逐层对ReLU函数进行松弛,然后将每层的ReLU函数输出控制在一个多边形范围内,进而得到整个神经网络的输出范围,并最终完成鲁棒性认证。
给定扰动范围,如果一个ReLU神经元输出的上界小于0或者下界大于0,我们称这个神经元是稳定的,因为它的输出总是线性的(\(z_i\)= 0 或者\(z_i = \hat{z}_i\))。对于稳定的神经元来说,输出的上界和下界是容易确定的。而对于非稳定的神经元,可以用如下的一组线性不等式进行松弛:
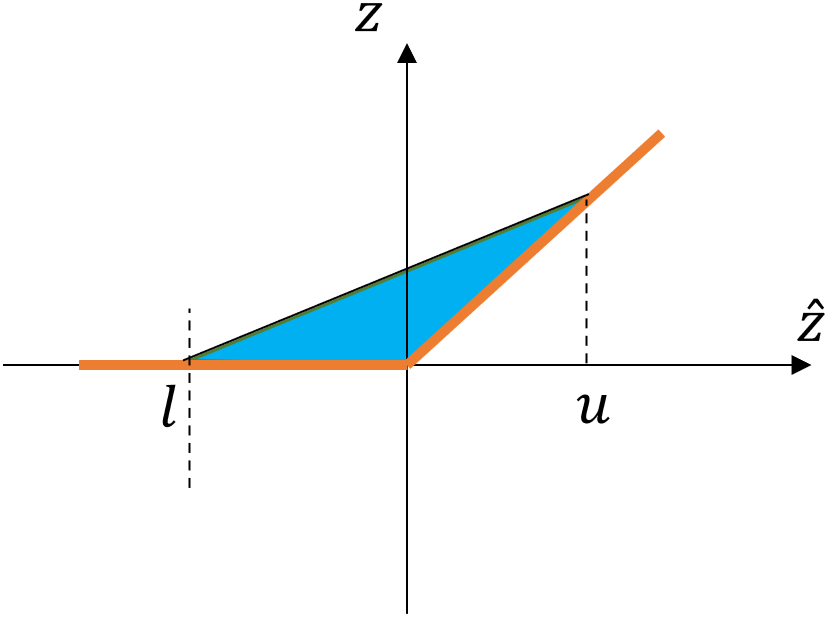
图7.5.1 松弛方式(a)(最紧凸松弛)¶
松弛后的ReLU输出如下图 图7.5.1 中蓝色区域所示。线性松弛后,鲁棒性认证即转化为一个多项式时间内可解的线性规划问题。 上述松弛方式是对ReLU函数的最紧凸松弛。LP-full认证方法 (Weng et al., 2018) 就是基于最紧凸松弛的方法,其逐层计算输出下界\(l\)和上界\(u\),并最终将问题转化为线性规划进行认证。虽然LP-full是多项式时间内可解的,但其需要对每个非稳定神经元进行松弛,所以计算代价依旧很大,认证在CIFAR-10数据集上训练的中等模型需要花费数天的时间,并且得到的鲁棒半径相对准确值仅有1.5-5的近似度,精确度比较低。
LP-full运算速度慢的一个重要原因是输出的三角形边界有两个下界(图 图7.5.1 三角形下面的两条边)需要传播。为了加快输出范围的传播,可以使用图 图7.5.2 所示的三种多边形边界进行松弛,这三种松弛方式使得ReLU函数的输出有着单一的下界。这种单一线性上下界的性质,使得ReLU函数的上下界可以高效地在神经网络的不同层之间进行前向传播。
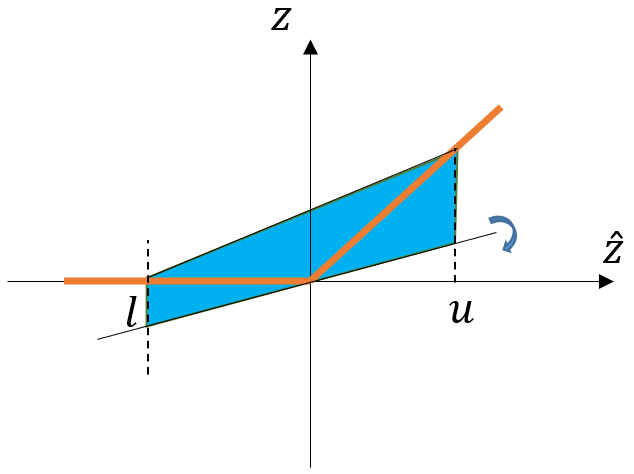
图7.5.2 更高效的松弛方式¶
在一个L层前馈ReLU神经网络中,假设第\(i\)层输出\(z_i( x)\)的上下界分别为\(l_{i} x + b_{i,l}\)和\(u_{i} x + b_{i,u}\),即\(l_{i} x + b_{i,l} < z_i( x) < u_{i} x + b_{i,u}\),且第\(i + 1\)层的仿射变换为\(\hat{ z}_{i + 1} = W_{i} z_{i} + b_{i}\),则ReLU输出的传播过程可形式化为:
其中,\(W_{i} ^ {+} = \max(W_i, 0)\),\(W_{i} ^ {-} = \min(W_i, 0)\)。这种线性上下界传播的方法,每次传播只需要进行四次矩阵乘法(即\(W_{i}^{+}l_{i}\)、\(W_{i}^{-}u_{i}\)、\(W_{i}^{+}u_{i}\)和\(W_{i}^{-}l_{i}\)),计算量跟模型推理在一个数量级上,所以与最紧凸松弛每次都需要求解线性规划问题相比,计算效率更高。
上文提到的CROWN算法就是综合采用了(b)、(c)、(d)这三种松弛方式:
可以看出,CROWN算法采用一个可变的线性下界来对ReLU函数进行松弛。此外,CROWN算法通过梯度上升的方法来优化下界的斜率\(\alpha\),取得了更好的认证效果。
为了进一步提高计算效率,Gowal等人 (Gowal et al., 2019) 提出了区间边界传播算法(interval bound propagation,IBP)。相比前面介绍的前向线性上下界传递来说,IBP的传播速度会更快。直观来讲,IBP直接在神经网络中逐层传递输出的上界\(u\)和下界\(l\),并不断对输出的上界和下界进行松弛。
若扰动的输入范围为\(B_{p, \epsilon}( x_0)\),则神经网络的第一层的输入的范围是\(z_1 = x \in [ x_0 - \epsilon, x_0 + \epsilon]\),\(z_1\)的范围也可以表示为\([l_1, u_1]\)。若神经网络第\(i\)层的输出范围为\([l_i, u_i]\),且第\(i+1\)层的变换为\(\hat{ z}_{i + 1} = W_{i} z_{i} + b_{i}\),则经过第\(i+1\)层变换后的上界\(\hat{u}_{i+1}\)和下界\(\hat{l}_{i+1}\)的传递过程可形式化如下:
易知,IBP算法的每次上下界传递也仅需四次矩阵-向量乘法运算。根据ReLU函数的定义,可以得到第\(i+1\)层的输出上下界松弛结果如下:
本质上,IBP也是对ReLU进行了线性松弛,其对应的松弛区域为一个矩形。上述几种线性松弛方式对ReLU函数的松弛程度都比较大,尤其是IBP算法,导致在多层传递后得到的上下界过于宽松。但在下文中我们会介绍,虽然IBP算法进行了最宽松的松弛,但是在结合了基于松弛的训练之后,却有着近似度最好的效果。所以松弛程度高并不一定意味着认证效果差,认证鲁棒性的过程是由认证算法和训练方式共同决定的。
以上方法通过不同的松弛不等式来实现不同程度的松弛,另一种思路则考虑一次松弛多个神经元从而加速松弛过程。Singh等人的研究 (Singh et al., 2019) 提出了一个新颖的框架k-ReLU,可以同时对多个神经元进行联合松弛,并且证明了在高维输入空间中多神经元松弛相对单神经元能获得更紧的边界。比如,当k=2 时,对\(z_1 := ReLU(\hat{ z}_1)\)和\(z_2 := ReLU(\hat{ z}_2)\)联合成\(z_3 := ReLU(\hat{ z}_1 + \hat{ z}_2)\), 然后在\(z_1 z_2\hat{ z}_1\hat{ z}_2\)空间中进行松弛运算。研究表明,在\(z_1 z_2\hat{ z}_1\hat{ z}_2\)空间中,联合ReLU神经元的凸松弛在\(\hat{ z}_1 + \hat{ z}_2\)方向能够获得更紧的边界 (Singh et al., 2019) 。根据推测,2-ReLU考虑到了两个神经元输入之间的约束关系,所以相对单输入神经元得到了更优的结果。同时,这种联合认证的方式也可以起到显著的加速效果。
上述几种线性松弛的鲁棒性认证算法都需要结合松弛训练进行使用。松弛训练是从对抗训练延伸出的一个概念。如章节 7.3节 所介绍,对抗训练是一个最小-最大化(min-max)问题:
其中,\(\mathcal{L}\)是常见的交叉熵损失函数。对于外层的最小化问题,一般使用梯度下降来解决(与模型训练一样)。但内层最大化问题往往是一个非凸优化问题,无法在多项式时间内求解。松弛训练使用线性松弛方法(逐层线性松弛、IBP算法、多输入神经元松弛以及其他松弛方法等)来代替内层非凸优化问题,利用线性松弛近似得到损失函数的最大值。
由于上述方法得到的结果是可微的,所以外层可以直接使用梯度下降优化这些界限。实验表明,尽管IBP算法的松弛在上述几种方法中是最宽松的,但是结合松弛训练,IBP却能取得最好的鲁棒性认证效果 (Jovanović et al., 2021) 。 结合松弛训练,IBP算法可以认证在CIFAR-10上训练的大模型和ImageNet上训练的小模型。
由于线性松弛的方法将鲁棒性认证转化为一个最优化问题,一些研究尝试解决其对应的拉格朗日对偶(Lagrange duality)问题 (Dvijotham et al., 2018, Dvijotham et al., 2018) ,但是根据 (Salman et al., 2019) 的研究,这些基于线性不等式的鲁棒性认证方法得到的认证结果界限并不会比最紧凸松弛更紧,这一限制被称为“凸障碍”(convex barrier)。
认证神经网络的鲁棒性除了可以对激活函数进行松弛以外,还可以基于模型所对应函数的本身性质如Lipschitz常数进行 (Lee et al., 2020, Leino et al., 2021, Tsuzuku et al., 2018) 。对于一个标量函数\(g:\mathbb{R}^{n} \supset \chi \to \mathbb{R}\),若\(\forall x_i, x_2 \in B_{p, \epsilon}( x_0)\),则我们定义函数\(g\)在区域\(B_{p, \epsilon}( x_0)\)中具有关于\(L_q\)-范数的局部Lipschitz常数\(L\),\(L\)满足如下条件:
Lipschitz常数类似函数在给定区域内导数值的上确界。计算神经网络中每一层的Lipschitz常数之后,可以利用这些常数的乘积来近似地认证模型的鲁棒性。例如,\(x\)为模型的输入,\(W_k\)是模型第\(k\)层的参数,\(\Phi( x)\)为模型的输出,\(\Phi_k( x)\)为第k层的运算,则:
根据上述定义,对给定扰动范围的任意两个输入\(x, x+r\),其输出的距离可以表示为:
其中,\(L = \prod_{k =1}^{K} L_k\),\(L_k\)为第\(k\)层函数的Lipschitz常数。受连乘带来的累积膨胀效应,通过这种方式计算得到的边界往往是非常宽松的,所以基于Lipschitz常数的认证方法往往需要在训练阶段对Lipschitz常数进行正则化。对于经过正则化的模型,全局Lipschitz常数能够有效地被用于鲁棒性认证,实验表明这种认证方法可以应用于ImageNet上训练的小模型 (Lee et al., 2020) 。
此外,可以通过设计更“平滑”(Lipschitz常数更小)的激活函数来提高Lipschitz认证方法的精确性。例如,一些研究者 (Li et al., 2019) 发现了一种“平滑层”的结构,通过构造一些正交的卷积层,可以使得这些层的Lipschitz常数为1甚至更小 (Hein and Andriushchenko, 2017) 。这些有上界的Lipschitz常数能更有效地估计神经网络的输出范围,不会得到过于宽松的边界,从而更有效地实现鲁棒性认证,但是这些方法只局限于\(L_2\)范数下的认证。Zhang等人 (Zhang et al., 2021) 设计了一种新的激活函数\(z = \Vert x- w \Vert_{\infty} + b\),并证明其可替代经典的“仿射变换+ReLU”操作。同时,此激活函数的Lipschitz常数在\(L_{\infty}\)范数下是小于等于1的,所以基于Lipschitz的认证方法可以很容易地应用在此类模型上来,带来\(L_{\infty}\)范数下的最优鲁棒性认证。
鲁棒性认证方法需要持续改进。对于线性松弛方法来说,找到一种松弛界限更紧同时又可以进行更大规模多神经元松弛的方法是未来的一个研究方向。其次,由于线性松弛的方法会产生指数级别的线性约束,如何在大量的线性约束中选择关键的约束也是很重要的一个议题。最后,如何优化松弛训练的过程也是研究者所关注的。而对于基于Lipschitz的认证方法来说,“平滑层”结构仍然有很大的研究空间,如何利用平滑层构造出更容易被认证的神经网络结构也是值得探索的一个方向。
7.5.4. 认证大模型¶
虽然近似认证算法可以加快认证速度,从而应用于更大的模型,但是这些算法还不能应对ImageNet规模的模型。 目前,只有基于随机平滑(randomized smoothing) (Yang et al., 2020) 的认证方法可以对ImageNet规模的模型进行认证。这种方法也被称为基于概率的方法,因为它并非直接在目标模型上进行鲁棒性认证,而是以添加随机噪声的方式对模型进行平滑,然后在平滑后的模型上进行鲁棒性认证,最后利用目标模型和平滑模型之间的相似性(迁移性),以一定概率完成对目标模型的鲁棒性认证。
随机平滑认证方法需要目标模型本身对噪声具有一定的鲁棒性,所以需要使用增强训练技术提升其鲁棒性。具体来说,增强训练在训练过程中向训练样本中添加(与认证)相同分布的噪声,并在添加了噪声的训练样本上进行模型训练。 在得到增强的模型之后,需要构造其对应的平滑模型。选择平滑分布\(\mu\),影响范围为\(supp(\mu)\),在\(\delta\)点的密度为\(\mu(\delta)\),则分类器\(f\)的平滑分类器\(f_{\text{smooth}}\)可定义如下:
其中,\(\mathbb{1}[\cdot]\)为指示器函数,\([C]\)为类别标签集合(\(C\)为总类别数)。因为上述积分无法精确计算,所以通常采用概率方法进行近似。对于任意输入样本\(x_0\),假设平滑模型以概率\(P_A = Pr_{\delta \thicksim \mu}[f( x_0 + \delta) = y_0]\)预测正确类别\(y_0\)(即概率最大的类别), 并且以第二大的概率\(P_B = \max_{y^{'} \in [C]: y^{'} \neq y_0} Pr_{\delta \thicksim \mu}[f( x_0 + \delta) = y']\)预测某个错误类别\(y'\)。通过蒙特卡洛抽样的方法,可以以很高的置信度得到\(P_A\)和\(P_B\)的取值区间。
因为增强的目标模型对噪声具有一定的鲁棒,所以当一个很接近\(x_0\)的对抗样本\(x'\)传入模型时,\(x_0+\delta\)和\(x'+\delta\)的分布也会很接近,并且上述计算得到的\(P_A'\)和\(P_{B}'\)也会接近\(P_A\)和\(P_B\)。所以当\(P_A\)和\(P_B\)之间的距离足够大时,\(P_A'\)也仍然会大于\(P_{B}'\), 即模型对对抗样本\(x'\)是鲁棒的。 以上只是对随机平滑认证的直观理解,Yang等人 (Yang et al., 2020) 利用Neyman-Pearson定理严格证明了基于高斯分布(Gaussian distribution)的平滑模型的\(L_2\)范数鲁棒性半径为:
其中,\(\Phi\)为高斯分布的累积分布函数(CDF),\(\sigma\)为高斯分布的标准差。
此外,基于拉普拉斯分布(Laplace distribution)可以完成\(L_1\)范数鲁棒性半径 (Li et al., 2019, Teng et al., 2020) ,证明思路与\(L_2\)类似。首先,基于拉普拉斯分布进行增强训练获得平滑模型,计算最大的正确分类概率\(P_A\)以及第大的错误分类概率\(P_B\)。然后根据加在平滑模型上的拉普拉斯分布,在\(P_A\)和\(P_B\)之间,估计出两个非鲁棒区域的边界,将非鲁棒区域用这两个边界进行放大,从而形成两个关于\(L_1\)鲁棒性半径的不等式。然后再根据概率积分确定两个关于鲁棒性半径的等式。最终根据得到的等式与不等式对鲁棒性半径进行估计。Teng等人 (Teng et al., 2020) 提出的基于拉普拉斯分布的随机平滑认证方法能够得到的\(L_1\)鲁棒性半径为:
对于随机平滑类的认证方法来说,平滑分布的选择是非常重要的,同一种认证算法往往可以选择不同的平滑分布来构造平滑分类器。对于\(L_2\)鲁棒性来说,研究者一般都会根据经验选择高斯分布。但是也有研究表明,一些替代方案能够取得比高斯分布更好的认证结果。而对于\(L_1\)鲁棒性,Yang等人 (Yang et al., 2020) 研究发现,使用均匀分布(uniform distribution)可以获得比拉普拉斯分布更好的认证结果。此外,选择具有较大方差的分布可以认证更大的鲁棒性半径,但是由于输入中的噪声比重会增大,所以认证的准确性会有所下降。另外,虽然可以利用蒙特卡洛方法来获得任意高置信度的认证结果,但是目标置信度越搞,对分类器的访问次数就会越多,时间开销也就越大。
目前,随机平滑算法能够认证的鲁棒性半径与完备认证算法相比还存在一定差距,所以设计更加精确的随机平滑认证算法仍然是一个挑战。同时,如何选择更优的平滑分布来生成平滑模型,从而完成不同范数下的鲁棒性认证也是一个重要的研究课题。关于增强训练,研究表明使用噪声增强与正则化相结合的方法可以得到更易于认证的模型 (Jeong and Shin, 2020) 。
由于随机平滑的方法不直接访问目标模型,所以容易拓展到前馈ReLU网络以外的其他网络结构 (Singh et al., 2019) ,并且可以应用于\(L_p\)范数之外的鲁棒性认证,比如对语义转换攻击进行鲁棒性认证 (Engstrom et al., 2018) 。随机平滑还可以进行分类任务之外的鲁棒性认证,比如对自然语言处理的神经网络模型进行鲁棒性认证 (Jia et al., 2019) 。如何将随机平滑认证方法更好地应用于更广泛的模型也是未来的研究方向。
7.6. 本章小结¶
本章节主要介绍了对抗防御方面的相关研究工作。章节 7.1节 介绍了关于对抗样本成因的五种经典解释,包括高度非线性假说、局部线性假说、边界倾斜假说、高维流行假说和不鲁棒特征假说。在这些成因解释的基础之上,我们在章节 7.2节 介绍了六类对抗样本检测方法,包括二级分类法、主成分分析法、异常分布检测法、预测不一致性、重建不一致性以及诱捕检测法。章节 7.3节 介绍了最主流、最有效的一种对抗防御方法,即对抗训练,从早期对抗训练方法出发先后介绍了PGD对抗训练、TRADES对抗训练等大量经典的对抗训练方法以及加速、大规模训练、鲁棒性蒸馏和鲁棒模型结构搜索等方法。章节 7.4节 介绍了另一类比较轻量级、灵活性高的防御方法,即输入空间防御,包括输入的去噪、压缩、随机变换、替换、修复等。最后,章节 7.5节 基于小模型、中模型和大模型等不同规模的模型,介绍了可认证防御相关的方法的基本思路。通过这些介绍,读者可以初步了解研究者们在对抗防御方面所作出的努力、现有防御方法的不足和未来的改进方向。
